
【题目】已知f(x)=log ![]() (x2﹣2x)的单调递增区间是( )
(x2﹣2x)的单调递增区间是( )
A.(1,+∞)
B.(2,+∞)
C.(﹣∞,0)
D.(﹣∞,1)
科目:高中数学 来源: 题型:
【题目】若函数f(x)的零点与g(x)=4x+2x﹣2的零点之差的绝对值不超过0.25,则f(x)可以是( )
A.f(x)=4x﹣1
B.f(x)=(x﹣1)2
C.f(x)=ex﹣1
D.f(x)=ln(x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F(x)=f(x)+f(﹣x)在区间 ![]() 是单调递减函数,将F(x)的图象按向量
是单调递减函数,将F(x)的图象按向量 ![]() 平移后得到函数G(x)的图象,则G(x)的一个单调递增区间是( )
平移后得到函数G(x)的图象,则G(x)的一个单调递增区间是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x| ![]() <3x<9},B={x|log2x>0}.
<3x<9},B={x|log2x>0}.
(1)求A∩B和A∪B;
(2)定义A﹣B={x|x∈A且xB},求A﹣B和B﹣A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x),g(x)分别是定义在R上的奇函数和偶函数,且f(x)+g(x)=3x .
(1)求 f(x),g(x);
(2)若对于任意实数t∈[0,1],不等式f(2t)+ag(t)<0恒成立,求实数a的取值范围;
(3)若存在m∈[﹣2,﹣1],使得不等式af(m)+g(2m)<0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,动点
的左、右焦点,动点![]() 在
在![]() 上,连结
上,连结![]() 并延长
并延长![]() 至
至![]() 点,使得
点,使得![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 为坐标原点,点
为坐标原点,点![]() ,连结
,连结![]() 交
交![]() 于
于![]() 点,若直线
点,若直线![]() 的斜率与直线
的斜率与直线![]() 的斜率存在且不为零,证明: 这两条直线的斜率之比为定值.
的斜率存在且不为零,证明: 这两条直线的斜率之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条宽为![]() 的两平行河岸有村庄
的两平行河岸有村庄![]() 和供电站
和供电站![]() ,村庄
,村庄![]() 与
与![]() 的直线距离都是
的直线距离都是![]() ,
, ![]() 与河岸垂直,垂足为
与河岸垂直,垂足为![]() 现要修建电缆,从供电站
现要修建电缆,从供电站![]() 向村庄
向村庄![]() 供电.修建地下电缆、水下电缆的费用分别是
供电.修建地下电缆、水下电缆的费用分别是![]() 万元
万元![]() 、
、![]() 万元
万元![]() .
.
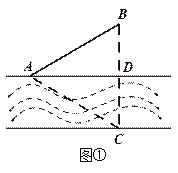
(1) 如图①,已知村庄![]() 与
与![]() 原来铺设有电缆
原来铺设有电缆![]() ,现先从
,现先从![]() 处修建最短水下电缆到达对岸后后,再修建地下电缆接入原电缆供电,试求该方案总施工费用的最小值;
处修建最短水下电缆到达对岸后后,再修建地下电缆接入原电缆供电,试求该方案总施工费用的最小值;
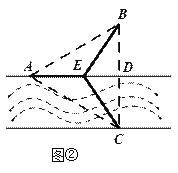
(2) 如图②,点![]() 在线段
在线段![]() 上,且铺设电缆的线路为
上,且铺设电缆的线路为![]() .若
.若![]() ,试用
,试用![]() 表示出总施工费用
表示出总施工费用![]() (万元)的解析式,并求
(万元)的解析式,并求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com