
【题目】为了解某市公益志愿者的年龄分布情况,有关部门通过随机抽样,得到如图1的频率分布直方图.
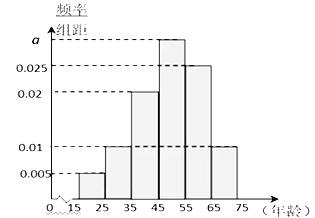
(1)求a的值,并估计该市公益志愿者年龄的平均数(同一组中的数据用该组区间的中点值作代表);
(2)根据世界卫生组织确定新的年龄分段,青年是指年龄15~44岁的年轻人.据统计,该市人口约为300万人,其中公益志愿者约占总人口的40%.试根据直方图估计该市青年公益志愿者的人数.
科目:高中数学 来源: 题型:
【题目】从金山区走出去的陈驰博士,在《自然—可持续性》杂志上发表的论文中指出:地球正在变绿,中国通过植树造林和提高农业效率,在其中起到了主导地位.已知某种树木的高度![]() (单位:米)与生长年限
(单位:米)与生长年限![]() (单位:年,tN*)满足如下的逻辑斯蒂函数:
(单位:年,tN*)满足如下的逻辑斯蒂函数:![]() ,其中e为自然对数的底数. 设该树栽下的时刻为0.
,其中e为自然对数的底数. 设该树栽下的时刻为0. ![]()
(1)需要经过多少年,该树的高度才能超过5米?(精确到个位)
(2)在第几年内,该树长高最快?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,直线l的参数方程为![]() (t为参数,
(t为参数,![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)当![]() 时,写出直线l的普通方程及曲线C的直角坐标方程;
时,写出直线l的普通方程及曲线C的直角坐标方程;
(2)已知点![]() ,设直线l与曲线C交于A,B两点,试确定
,设直线l与曲线C交于A,B两点,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面为矩形,且AB=![]() ,BC=1,E,F分别为AB,PC中点.
,BC=1,E,F分别为AB,PC中点.

(1)求证:EF∥平面PAD;
(2)若平面PAC⊥平面ABCD,求证:平面PAC⊥平面PDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系内,已知点![]() 及线段
及线段![]() ,在线段
,在线段![]() 上任取一点
上任取一点![]() ,线段
,线段![]() 长度的最小值称为“点
长度的最小值称为“点![]() 到线段
到线段![]() 的距离”,记为
的距离”,记为![]() .
.
(1)设点![]() ,线段
,线段![]()
![]() ,求
,求![]() ;
;
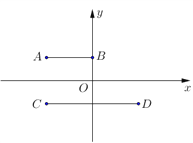
(2)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,线段
,线段![]() ,线段
,线段![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出该函数的值域.
的函数解析式,并写出该函数的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() =1(b∈N)的两个焦点F1、F2,P为双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.
=1(b∈N)的两个焦点F1、F2,P为双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com