
【题目】设函数f(x)=x2-ax+b,问:(1)讨论函数f(sinx)在( ![]() ,
, ![]() )内的单调性并判断有无极值,有极值时求出极值;(2)记f0(x)=
)内的单调性并判断有无极值,有极值时求出极值;(2)记f0(x)= ![]() -
- ![]() x +
x + ![]() ,求函数| f ( sin x ) -
,求函数| f ( sin x ) - ![]() ( sin x )| 在[
( sin x )| 在[ ![]() .
. ![]() ]上的最大值D,(3)在(2)中,取a0=b0=0,求z= b -
]上的最大值D,(3)在(2)中,取a0=b0=0,求z= b - ![]() 满足D ≤ 1时的最大值
满足D ≤ 1时的最大值
(1)讨论函数f(sinx)在(![]() ,
, ![]() )内的单调性并判断有无极值,有极值时求出极值;
)内的单调性并判断有无极值,有极值时求出极值;
(2)记f0(x)=![]() ,求函数
,求函数![]() 在
在![]() 上的最大值D,
上的最大值D,
(3)在(2)中,取a0=b0=0,求z=![]() 满足D
满足D![]() 1时的最大值
1时的最大值
【答案】
(1)
解:f(sinx)=sin2x-asinx+b=sinx(sinx-a)+b,![]() ,
,![]() =(2sinx-a)cosx,
=(2sinx-a)cosx,![]()
①当a![]() -2,b
-2,b![]() R时,函数f(sinx)单调递增,无极值
R时,函数f(sinx)单调递增,无极值
②当a![]() ,b
,b![]() R时,函数f(sinx)单调递减,无极值
R时,函数f(sinx)单调递减,无极值
③当-2![]() a
a![]() 2,在(
2,在(![]() ,
,![]() )内存在唯一的x0,是得2sinx=a,-
)内存在唯一的x0,是得2sinx=a,-![]()
![]() x
x![]() x0时,函数f(sinx)单调递增;X0
x0时,函数f(sinx)单调递增;X0![]() X
X![]()
![]() 时,函数f(sinx)单调递增,因此,-2
时,函数f(sinx)单调递增,因此,-2![]() a
a![]() 2,b
2,b![]() R时,函数f(x)在X0处有极小值f(sinX0)=f(
R时,函数f(x)在X0处有极小值f(sinX0)=f(![]() )=
)=![]()
(2)
解:![]() 时,
时,![]() =(a0-a)sinx+b-b0
=(a0-a)sinx+b-b0![]()
![]() .当
.当![]()
![]() 0时,取x=
0时,取x=![]() ,等号成立。当
,等号成立。当![]()
![]() 0时,取x=-
0时,取x=-![]() ,等号成立,由此可知最大值为D=
,等号成立,由此可知最大值为D=![]() +
+![]()
(3)D![]() 1,即
1,即![]() +
+![]()
![]() 1,此时0
1,此时0![]() a2
a2![]() 1,-1
1,-1![]() b
b![]() 1,从而z=b-
1,从而z=b-![]()
![]() 1
1
(3)
解:D![]() 1,即
1,即![]() +
+![]()
![]() 1,此时0
1,此时0![]() a2
a2![]() 1,-1
1,-1![]() b
b![]() 1,从而z=b-
1,从而z=b-![]()
![]() 1
1
取a=0,b=1.则![]() +
+![]()
![]() 1,并且z=b-
1,并且z=b-![]() =1.由此可知,z=
=1.由此可知,z=![]() 满足条件D
满足条件D![]() 1的最大值为1
1的最大值为1
【解析】函数导数解答题中贯穿始终的是数学思想方法,在含有参数的试题中,分类与整合思想是必要的,由于是函数问题,所以函数思想、数形结合思想也是必要的,把不等式问题转化为最值问题,把方程的根转化为零点问题等,转化与化归思想也起着同样的作用,解决函数、导数的解答题要充分,注意数学思想方法的应用。
【考点精析】通过灵活运用函数的单调性和二次函数在闭区间上的最值,掌握注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种;当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】一个二元码是由0和1组成的数字![]() 其中
其中![]() 称为第k位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)已知某中二元码
称为第k位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)已知某中二元码![]() 的码元满足如下校验方程组:
的码元满足如下校验方程组: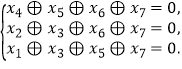 其中运算
其中运算![]() 定义为:
定义为:![]() 现已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了1101101,那么利用上述校验方程组可判定k等于 。
现已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了1101101,那么利用上述校验方程组可判定k等于 。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
(I)估计顾客同时购买乙和丙的概率;
(II)估计顾客在甲、乙、丙、丁中同时购买3中商品的概率;
(III)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(1)求y关于t的回归方程![]()
(2)用所求回归方程预测该地区2015年(![]() )的人民币储蓄存款.
)的人民币储蓄存款.
附:回归方程![]() 中
中
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 设x3+ax+b=0,其中a,b均为实数,下列条件中,使得该三次方程中仅有一个实根的是 ,(写出所有正确条件的编号)
设x3+ax+b=0,其中a,b均为实数,下列条件中,使得该三次方程中仅有一个实根的是 ,(写出所有正确条件的编号)
1、a=-3,b=-3;2.a=-3,b=2;3、a=-3,b![]() 2;4、a=0,b=2;5、a=1,b=2
2;4、a=0,b=2;5、a=1,b=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)在直角坐标系xOy中,直线l的参数方程为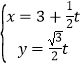 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,
(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,![]() c的极坐标方程为
c的极坐标方程为![]() =2
=2![]() sin
sin![]() .
.
(1)写出![]() c的直角坐标方程;
c的直角坐标方程;
(2)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若将函数y=2sin 2x的图像向左平移 ![]() 个单位长度,则评议后图象的对称轴为( )
个单位长度,则评议后图象的对称轴为( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点 (Ⅰ)求证:平面PAB⊥平面CDE;
(Ⅱ)若直线PC与平面PAD所成角为45°,求二面角A﹣DE﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com