
 某地产开发公司拟在如图所示夹角为60°的角形区域BAC内进行地产开发.根据市政要求,此地产开发必须在角形区域的两边之间建一条定长为500m的绿化带PQ,并且规定由此绿化带和角形区域围成的△APQ的面积作为此开发商的开发面积.问开发商如何给P,Q进行选址,才能使自己的开发面积最大?并求最大开发面积.
某地产开发公司拟在如图所示夹角为60°的角形区域BAC内进行地产开发.根据市政要求,此地产开发必须在角形区域的两边之间建一条定长为500m的绿化带PQ,并且规定由此绿化带和角形区域围成的△APQ的面积作为此开发商的开发面积.问开发商如何给P,Q进行选址,才能使自己的开发面积最大?并求最大开发面积.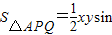 60°,从模型来看,面积的变化受xy的影响,所以再建立xy最大值模型,由余弦定理可知:5002=x2+y2-2xycos60°≥2xy-2xycos60°=xy,即xy≤5002,所以
60°,从模型来看,面积的变化受xy的影响,所以再建立xy最大值模型,由余弦定理可知:5002=x2+y2-2xycos60°≥2xy-2xycos60°=xy,即xy≤5002,所以 60°≤
60°≤ =62500
=62500 ,当且仅当x=y时取等号.即△APQ的面积最大.
,当且仅当x=y时取等号.即△APQ的面积最大.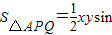 60°≤
60°≤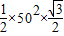 =62500
=62500 ,
,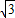 m2.(14分)
m2.(14分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
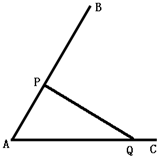 某地产开发公司拟在如图所示夹角为60°的角形区域BAC内进行地产开发.根据市政要求,此地产开发必须在角形区域的两边之间建一条定长为500m的绿化带PQ,并且规定由此绿化带和角形区域围成的△APQ的面积作为此开发商的开发面积.问开发商如何给P,Q进行选址,才能使自己的开发面积最大?并求最大开发面积.
某地产开发公司拟在如图所示夹角为60°的角形区域BAC内进行地产开发.根据市政要求,此地产开发必须在角形区域的两边之间建一条定长为500m的绿化带PQ,并且规定由此绿化带和角形区域围成的△APQ的面积作为此开发商的开发面积.问开发商如何给P,Q进行选址,才能使自己的开发面积最大?并求最大开发面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com