
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若![]() 为
为![]() 的极小值点,求
的极小值点,求![]() 的取值范围.
的取值范围.
【答案】(1)递增区间为![]() ,递减区间为
,递减区间为![]() (2)
(2)![]()
【解析】
(1)首先求出函数的导函数![]() ,记
,记![]() ,则
,则![]() ,分析
,分析![]() 的单调性,即可求出函数的单调性;
的单调性,即可求出函数的单调性;
(2)依题意可得![]() ,记
,记![]() ,则
,则![]() .
.
再令![]() ,则
,则![]() ,利用导数分析
,利用导数分析![]() 的单调性,即可得到
的单调性,即可得到![]() 在
在![]() 有零点,即
有零点,即![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,所以
单调递增,所以![]() ,再对
,再对![]() 分类讨论可得;
分类讨论可得;
解:(1)当![]() 时,
时,![]() ,
,
记![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
所以![]() ,
,
因为![]() ,所以
,所以![]() 在
在![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 为减函数.
为减函数.
综上所述,![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]() .·
.·
(2)由题意可得![]() ,
,![]() .
.
记![]() ,则
,则![]() .
.
再令![]() ,则
,则![]() .
.
下面证明![]() 在
在![]() 有零点:
有零点:
令![]() ,则
,则![]() 在
在![]() 是增函数,所以
是增函数,所以![]() .
.
又![]() ,
,![]() ,
,
所以存在![]() ,
,![]() ,且当
,且当![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数,
为增函数,
又![]() ,
,![]() ,所以
,所以![]() ,
,
根据零点存在性定理,存在![]() ,
,![]()
所以当![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
所以![]() ,即
,即![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
所以![]() .
.
①当![]() ,
,![]() ,
,![]() 恒成立,所以
恒成立,所以![]() ,即
,即![]() 为增函数,
为增函数,
又![]() ,所以当
,所以当![]() ,
,![]() ,
,![]() 为减函数,
为减函数,![]() ,
,![]() ,
,![]() 为增函数,
为增函数,![]() 是
是![]() 的极小值点,所以
的极小值点,所以![]() 满足题意.
满足题意.
②当![]() ,
,![]() ,令
,令![]() ,
,![]()
因为![]() ,所以
,所以![]() ,
,
故![]() 在
在![]() 单调递增,故
单调递增,故![]() ,即有
,即有![]()
故![]() ,
,
又![]() 在
在![]() 单调递增,
单调递增,
由零点存在性定理知,存在唯一实数![]() ,
,![]() ,
,
当![]() ,
,![]() ,
,![]() 单调递减,即
单调递减,即![]() 递减,
递减,
所以![]() ,
,
此时![]() 在
在![]() 为减函数,所以
为减函数,所以![]() ,不合题意,应舍去.
,不合题意,应舍去.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得-1分 . 现从盒内任取3个球
(Ⅰ)求取出的3个球中至少有一个红球的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设![]() 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上的动点,且
上的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)若![]() 是椭圆
是椭圆![]() 的左、右顶点,直线
的左、右顶点,直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)某县一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨、硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨、硝酸盐15吨.先库存磷酸盐10吨、硝酸盐66吨,在此基础上生产这两种混合肥料.若生产1车皮甲种肥料产生的利润为10000元;生产1车皮乙种肥料产生的利润为5000元.那么分别生产甲、乙两种肥料各多少车皮能产生最大的利润?
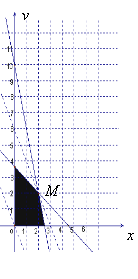
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,离心率为
,离心率为![]() ,双曲线
,双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,已知
,已知![]() ,
,![]() .
.
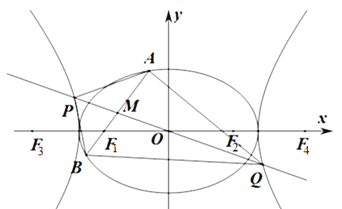
(1)求![]() ,
,![]() 的方程;
的方程;
(2)过![]() 作
作![]() 的不垂直于
的不垂直于![]() 轴的弦
轴的弦![]() ,
,![]() 为弦
为弦![]() 的中点,当直线
的中点,当直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点时,求四边形
两点时,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】车工刘师傅利用数控车床为某公司加工一种高科技易损零件,对之前加工的100个零件的加工时间进行统计,结果如下:
加工1个零件用时 | 20 | 25 | 30 | 35 |
频数(个) | 15 | 30 | 40 | 15 |
以加工这100个零件用时的频率代替概率.
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘师傅准备给几个徒弟做一个加工该零件的讲座,用时40分钟,另外他打算在讲座前、讲座后各加工1个该零件作示范.求刘师傅讲座及加工2个零件作示范的总时间不超过100分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,
,![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为
为![]() 上的动点,
上的动点,![]() 为
为![]() 的中点.
的中点.
(1)请求出![]() 点轨迹
点轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() 若直线
若直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() ,弦
,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖是十二地支的形象化代表,即子(鼠)、丑(牛)、寅(虎)、卯(兔)、辰(龙)、巳(蛇)、午(马)、未(羊)、申(猴)、酉(鸡)、戌(狗)、亥(猪),每一个人的出生年份对应了十二种动物中的一种,即自己的属相.现有印着六种不同生肖图案(包含马、羊)的毛绒娃娃各一个,小张同学的属相为马,小李同学的属相为羊,现在这两位同学从这六个毛绒娃娃中各随机取一个(不放回),则这两位同学都拿到自己属相的毛绒娃娃的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com