
【题目】在△ABC中,a、b、c分别是角A、B、C的对边,且 ![]() ,
,
(1)求角B的大小;
(2)若 ![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】
(1)解:由正弦定理 ![]() 得:
得:
a=2RsinA,b=2RsinB,c=2RsinC,
将上式代入已知 ![]() ,
,
即2sinAcosB+sinCcosB+cosCsinB=0,
即2sinAcosB+sin(B+C)=0,
∵A+B+C=π,
∴sin(B+C)=sinA,
∴2sinAcosB+sinA=0,即sinA(2cosB+1)=0,
∵sinA≠0,∴ ![]() ,
,
∵B为三角形的内角,∴ ![]() ;
;
(2)解:将 ![]() 代入余弦定理b2=a2+c2﹣2accosB得:
代入余弦定理b2=a2+c2﹣2accosB得:
b2=(a+c)2﹣2ac﹣2accosB,即 ![]() ,
,
∴ac=3,
∴ ![]()
【解析】(1)根据正弦定理表示出a,b及c,代入已知的等式,利用两角和的正弦函数公式及诱导公式变形后,根据sinA不为0,得到cosB的值,由B的范围,利用特殊角的三角函数值即可求出角B的度数;(2)由(1)中得到角B的度数求出sinB和cosB的值,根据余弦定理表示出b2,利用完全平方公式变形后,将b,a+c及cosB的值代入求出ac的值,然后利用三角形的面积公式表示出△ABC的面积,把ac与sinB的值代入即可求出值.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={(x,y)|x2+(y+1)2≤1},B={(x,y)| ![]() x+y=4m},命题P:A∩B=,命题q:直线
x+y=4m},命题P:A∩B=,命题q:直线 ![]() +
+ ![]() =1在两坐标轴上的截距为正.
=1在两坐标轴上的截距为正.
(1)若命题P为真命题,求实数m的取值范围;
(2)若“p∨q”为真,“p∧q”为假,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,点M是平面A1B1C1D1内一点,且BM∥平面ACD1 , 则tan∠DMD1的最大值为( ) 
A.![]()
B.1
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图△ABC是等腰三角形,BA=BC,DC⊥平面ABC,AE∥DC,若AC=2且BE⊥AD,则( ) 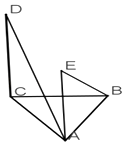
A.AB+BC有最大值
B.AB+BC有最小值
C.AE+DC有最大值
D.AE+DC有最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正项数列{an}满足: ![]() =an+1﹣an(a∈N*),则称此数列为“比差等数列”.
=an+1﹣an(a∈N*),则称此数列为“比差等数列”.
(1)请写出一个“比差等数列”的前3项的值;
(2)设数列{an}是一个“比差等数列”
(i)求证:a2≥4;
(ii)记数列{an}的前n项和为Sn , 求证:对于任意n∈N*,都有Sn> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 与动直线
与动直线![]() 的交点为
的交点为![]() ,线段
,线段![]() 的中垂线与动直线
的中垂线与动直线![]() 的交点为
的交点为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过动点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() ,求证:
,求证: ![]() 的大小为定值.
的大小为定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为ɑ 的正方体ABCD﹣A1B1C1D1中,E、F、G分别是CB.CD.CC1的中点. 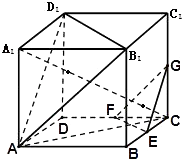
(1)求直线 A1C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子装有六张卡片,上面分别写着如下六个函数: ![]() .
.
(I)判断这![]() 个函数的奇偶性;
个函数的奇偶性;
(II)从中任意拿取两张卡片,若其中至少有一张卡片上写着的函数为奇函数.在此条件下,求两张卡片上写着的函数相加得到的新函数为奇函数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com