解:(I)因为
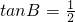
,
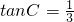
,
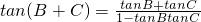
,(1分)
代入得到,
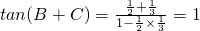
.(3分)
因为A=180°-B-C,(4分)
所以tanA=tan(180°-(B+C))
=-tan(B+C)=-1.(5分)
(II)因为0°<A<180°,由(I)结论可得:A=135°.(7分)
因为
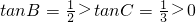
,
所以0°<C<B<90°.(8分)
所以sinB=
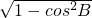
=
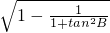
=

,sinC=
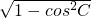
=
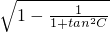
=

,(9分)
由c=1及
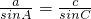
得:
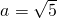
,(11分)
所以△ABC的面积S=
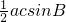
=

×1×

×

=

.(13分)
分析:(Ⅰ)利用两角和的正切函数公式表示出tan(B+C),把tanB和tanC的值代入即可求出tan(B+C)的值,根据三角形的内角和定理及诱导公式得到tanA等于-tan(B+C),进而得到tanA的值;
(Ⅱ)由(I)求出的tanA的值,由A的范围,利用特殊角的三角函数值即可求出A的度数,再由tanB和tanC的值,得到B和C的范围及大小关系,利用同角三角函数间的基本关系分别求出sinB和sinC的值,由c的值,sinB和sinC的值,利用正弦定理即可求出a的值,利用三角形的面积公式表示出三角形ABC的面积,把a,c和sinB的值代入即可求出面积.
点评:此题考查学生灵活运用两角和的正切函数公式,同角三角函数间的基本关系化简求值,灵活运用正弦定理及三角形的面积公式化简求值,是一道中档题.学生做题时注意利用tanB和tanC的值确定出B和C的范围及大小.

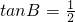 ,
,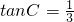 ,且c=1.
,且c=1.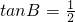 ,
,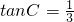 ,
,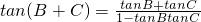 ,(1分)
,(1分)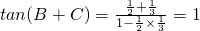 .(3分)
.(3分)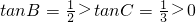 ,
,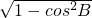 =
=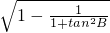 =
= ,sinC=
,sinC=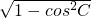 =
=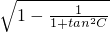 =
= ,(9分)
,(9分)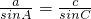 得:
得: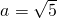 ,(11分)
,(11分)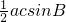 =
= ×1×
×1× ×
× =
= .(13分)
.(13分)
