
【题目】函数f(x)=|x+3|+|x﹣1|,其最小值为t.
(1)求t的值;
(2)若正实数a,b满足a+b=4,求证 ![]() .
.
【答案】
(1)解:解法1: 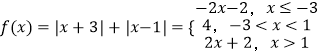 ,由函数的图象知最小值t=4
,由函数的图象知最小值t=4
解法2:由绝对值三角不等式,得f(x)=|x+3|+|x﹣1|≥|(x+3)﹣(x﹣1)|=4,即t=4.
(2)证明:(解法1)基本不等式】a+b=4,所以 ![]() ,
,
当且仅当 ![]() ,即
,即 ![]() 时取等号.所以
时取等号.所以 ![]() .
.
(解法2)柯西不等式】因为a+b=4,所以 ![]() ,∴
,∴ ![]() 当且仅当
当且仅当 ![]() ,即
,即 ![]() 时取等号.所以
时取等号.所以 ![]() .
.
【解析】本题分两个小题,(1)考查绝对值不等式,方法一运用不等式的定义进行化简,使用数形结合思想求得最小值;方法二使用绝对值三角不等式,更加简单明了。(2)考查不等式的证明,方法一给原式左边乘以![]() ,展开后使用基本不等式求出最小值,从而证明。方法二使用柯西不等式,直接简单。注意等号成立的条件。
,展开后使用基本不等式求出最小值,从而证明。方法二使用柯西不等式,直接简单。注意等号成立的条件。


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)经过点(
=1(a>b>0)经过点( ![]() ,﹣
,﹣ ![]() ),且椭圆的离心率e=
),且椭圆的离心率e= ![]() .
.
(1)求椭圆的方程;
(2)过椭圆的右焦点F作两条互相垂直的直线,分别交椭圆于点A,C及B,D,设线段AC,BD的中点分别为P,Q.求证:直线PQ恒过一个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆G: ![]() +y2=1,与x轴不重合的直线l经过左焦点F1 , 且与椭圆G相交于A,B两点,弦AB的中点为M,直线OM与椭圆G相交于C,D两点.
+y2=1,与x轴不重合的直线l经过左焦点F1 , 且与椭圆G相交于A,B两点,弦AB的中点为M,直线OM与椭圆G相交于C,D两点.
(1)若直线l的斜率为1,求直线OM的斜率;
(2)是否存在直线l,使得|AM|2=|CM||DM|成立?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右顶点为
的右顶点为 ![]() ,离心率为
,离心率为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过右焦点F且斜率不为0的动直线l与椭圆交于M,N两点,过M作直线x=a2的垂线,垂足为M1 , 求证:直线M1N过定点,并求出定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
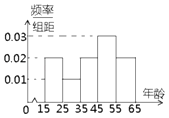
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填2×2列联表,并判断是否95%的把握认为以45岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动,现从这8人中随机抽2人.
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率;
②记抽到45岁以上的人数为X,求随机变量X的分布列及数学期望.
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设公比不为1的等比数列{an}的前n项和Sn , 已知a1a2a3=8,S2n=3(a1+a3+a5+…+a2n﹣1)(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=(﹣1)nlog2an , 求数列{bn}的前2017项和T2017 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=a(x﹣1)2﹣xe2﹣x .
(Ⅰ)若曲线y=f(x)在点(2,f(2))处的切线与x轴平行,求a的值;
(Ⅱ)若 ![]() ,求f(x)的单调区间.
,求f(x)的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com