[题目]在△ABC中“sinA>sinB 是“cosA<cosB 的( )A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】在△ABC中“sinA>sinB”是“cosA<cosB”的（）

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分也不必要条件

【答案】

【解析】试题解析：必要性在△ABC中，“cosA＞cosB”，由余弦函数在（0，π）是减函数，故有A＜B，

若B不是钝角，显然有“sinA＜sinB”成立，

若B是钝角，因为A+B＜π，故有A＜π-B＜，故有sinA＜sin（π-B）=sinB

综上，“cosA＞cosB”可以推出“sinA＜sinB”：

充分性：由“sinA＜sinB”

若B是钝角，在△ABC中，显然有0＜A＜B＜π，可得，“cosA＞cosB”

若B不是钝角，显然有0＜A＜B＜，此时也有cosA＞cosB

综上，“sinA＜sinB”推出“cosA＞cosB”成立

故，“cosA＞cosB”是“sinA＜sinB”的充要条件

练习册系列答案

康华传媒考出好成绩中考试题汇编系列答案

寒假作业甘肃教育出版社系列答案

中考211系列答案

寒假生活四川大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】条形码是将宽度不等的多个黑条和空白，按照一定的编码规则排列，用以表达一组信息的图形标识符。常见的条形码是“”通用代码，它是由从左到右排列的13个数字（用表示）组成，其中是校验码，用来校验前12个数字代码的正确性.下面的框图是计算第13位校验码的程序框图，框图中符号表示不超过的最大整数(例如).现有一条形码如图（1)所示,其中第6个数被污损，那么这个被污损数字是（）

A. 6 B. 7 C. 8 D. 9

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）＝x，g（x）＝x－4，则下列结论正确的是（）

A.若h（x）＝f（x）g（x），则函数h（x）的最小值为4

B.若h（x）＝f（x）|g（x）|，则函数h（x）的值域为R

C.若h（x）＝|f（x）|－|g（x）|，则函数h（x）有且仅有一个零点

D.若h（x）＝|f（x）|－|g（x）|，则|h（x）|≤4恒成立

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为回馈顾客，新华都购物商场拟通过摸球兑奖的方式对500位顾客进行奖励，规定：每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球（球的大小、形状一模一样），球上所标的面值之和为该顾客所获的奖励额.

（1）若袋中所装的4个球中有1个所标的面值为40元，其余3个所标的面值均为20元，求顾客所获的奖励额的分布列及数学期望；

（2）商场对奖励总额的预算是30000元，并规定袋中的4个球由标有面值为20元和40元的两种球共同组成，或标有面值为15元和45元的两种球共同组成．为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡．请对袋中的4个球的面值给出一个合适的设计，并说明理由．

提示：袋中的4个球由标有面值为a元和b元的两种球共同组成，即袋中的4个球所标的面值“既有a元又有b元”．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，四棱锥P﹣ABCD中，PD⊥底面ABCD，底面ABCD是边长为a的正方形，且PD=a．

（1）求四棱锥P﹣ABCD的体积；

（2）若E为PC中点，求证：PA∥平面BDE；

（3）求直线PB与平面ABCD所成角的正切值．

查看答案和解析>>

科目：高中数学 来源： 题型：

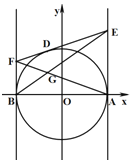
【题目】如图所示，圆O：，，，D为圆O上任意一点，过D作圆O的切线分别交直线和于E，F两点，连AF，BE交于点G，若点G形成的轨迹为曲线C．

记AF，BE斜率分别为，，求的值并求曲线C的方程；

设直线l：与曲线C有两个不同的交点P，Q，与直线交于点S，与直线交于点T，求的面积与面积的比值的最大值及取得最大值时m的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某房产中介公司2017年9月1日正式开业，现对其每个月的二手房成交量进行统计，表示开业第个月的二手房成交量，得到统计表格如下：

（1）统计中常用相关系数来衡量两个变量之间线性关系的强弱.统计学认为，对于变量，如果，那么相关性很强；如果，那么相关性一般；如果，那么相关性较弱.通过散点图初步分析可用线性回归模型拟合与的关系.计算的相关系数，并回答是否可以认为两个变量具有很强的线性相关关系（计算结果精确到0.01）

（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程（计算结果精确到0.01），并预测该房产中介公司2018年6月份的二手房成交量（计算结果四舍五入取整数）.

（3）该房产中介为增加业绩，决定针对二手房成交客户开展抽奖活动.若抽中“一等奖”获6千元奖金；抽中“二等奖”获3千元奖金；抽中“祝您平安”，则没有奖金.已知一次抽奖活动中获得“一等奖”的概率为，获得“二等奖”的概率为，现有甲、乙两个客户参与抽奖活动，假设他们是否中奖相互独立，求此二人所获奖金总额（千元）的分布列及数学期望.