已知数列{an}的前n项和为Sn,点(an+2,Sn+1)在直线y=4x-5上,其中n∈N*,令bn=an+1-2an,且a1=1.
(1)求数列{bn}的通项公式;
(2)若f(x)=b1x+b2x2+b3x3+…+bnxn,求f?(1)的表达式,并比较f?(1)与8n2-4n的大小.
解:(1)∵S
n+1=4(a
n+2)-5,
∴S
n+1=4a
n+3.
∴S
n=4a
n-1+3(n≥2).
∴a
n+1=4a
n-4a
n-1(n≥2).
∴a
n+1-2a
n=2(a
n-2a
n-1)(n≥2).
∴
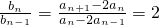
(n≥2).
∴数列{b
n}为等比数列,其公比为q=2,首项b
1=a
2-2a
1,
而a
1+a
2=4a
1+3,且a
1=1,
∴a
2=6.
∴b
1=6-2=4.
∴b
n=4×2
n-1=2
n+1.(4分).
(2)∵f(x)=b
1x+b
2x
2+b
3x
3++b
nx
n,
∴f'(x)=b
1x+2b
2x+3b
3x
2++nb
nx
n-1.
∴f'(1)=b
1+2b
2+3b
3++nb
n.
∴f'(1)=2
2+2•2
3+3•2
4++n•2
n+1,①
∴2f'(1)=2
3+2•2
4+3•2
5++n•2
n+2.②
①-②得-f'(1)=2
2+2
3+2
4++2
n+1-n•2
n+2=
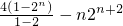
=-4(1-2
n)-n•2
n+2,
∴f'(1)=4+(n-1)•2
n+2.(6分).
∴f'(1)-(8n
2-4n)=4(n-1)•2
n-4(2n
2-n-1)=4(n-1)[2
n-(2n+1)].
当n=1时,f′(1)=8n
2-4n;
当n=2时,f′(1)-(8n
2-4n)=4(4-5)=-4<0,f′(1)<8n
2-4n;
当n≥3时,4(n-1)>0,
且2
n=(1+1)
n=C
n0+C
n1+C
nn-1+C
nn>2n+2>2n+1,
∴n≥3时,总有2
n>2n+1.(10分).
∴n≥3时,总有f′(1)>8n
2-4n.
分析:(1)由S
n+1=4(a
n+2)-5,知S
n=4a
n-1+3(n≥2).所以a
n+1=4a
n-4a
n-1(n≥2).a
n+1-2a
n=2(a
n-2a
n-1)(n≥2),
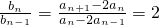
(n≥2).由此能求出数列{b
n}的通项公式;
(2)由f(x)=b
1x+b
2x
2+b
3x
3++b
nx
n,知f'(1)=b
1+2b
2+3b
3+…+nb
n=2
2+2•2
3+3•2
4+…+n•2
n+1,再由错位相减法能够导出f'(1)=4+(n-1)•2
n+2.然且由分类讨论进行求解.
点评:本题考查数列的性质和应用,解题时要注意公式的合理运用,注意错位相减法和分类讨论思想的运用.

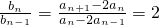 (n≥2).
(n≥2).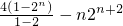 =-4(1-2n)-n•2n+2,
=-4(1-2n)-n•2n+2,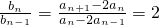 (n≥2).由此能求出数列{bn}的通项公式;
(n≥2).由此能求出数列{bn}的通项公式;

 阅读快车系列答案
阅读快车系列答案