
 某售货员负责在甲、乙、丙三个柜面上售货.如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8,0.7.假定各个柜面是否需要照顾相互之间没有影响,求在这个小时内:
某售货员负责在甲、乙、丙三个柜面上售货.如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8,0.7.假定各个柜面是否需要照顾相互之间没有影响,求在这个小时内: 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
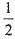 ,通晓中文和日语的概率为
,通晓中文和日语的概率为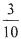 .若通晓中文和韩语的人数不超过3人.
.若通晓中文和韩语的人数不超过3人.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 正常工作的概率分别为
正常工作的概率分别为 ,将它们中某两个元件并联后再和第三个元件串联接入电路,在如图的电路中,电路不发生故障的概率是 ( )
,将它们中某两个元件并联后再和第三个元件串联接入电路,在如图的电路中,电路不发生故障的概率是 ( )
A.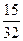 | B. | C.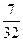 | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com