
【题目】原命题:“![]() ,
, ![]() 为两个实数,若
为两个实数,若![]() ,则
,则![]() ,
, ![]() 中至少有一个不小于1”,下列说法错误的是( )
中至少有一个不小于1”,下列说法错误的是( )
A. 逆命题为:若![]() ,
, ![]() 中至少有一个不小于1,则
中至少有一个不小于1,则![]() ,为假命题
,为假命题
B. 否命题为:若![]() ,则
,则![]() ,
, ![]() 都小于1,为假命题
都小于1,为假命题
C. 逆否命题为:若![]() ,
, ![]() 都小于1,则
都小于1,则![]() ,为真命题
,为真命题
D. “![]() ”是“
”是“![]() ,
, ![]() 中至少有一个不小于1”的必要不充分条件
中至少有一个不小于1”的必要不充分条件
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
分组 | 频数 |
[2,4) | 2 |
[4,6) | 10 |
[6,8) | 16 |
[8,10) | 8 |
[10,12] | 4 |
合计 | 40 |
(1)求频率分布直方图中a,b的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①函数 ![]() 是奇函数;
是奇函数;
②存在实数α,使得sinα+cosα= ![]() ;
;
③若α,β是第一象限角且α<β,则tanα<tanβ;
④ ![]() 是函数
是函数 ![]() 的一条对称轴方程;
的一条对称轴方程;
⑤函数 ![]() 的图象关于点
的图象关于点 ![]() 成中心对称图形.
成中心对称图形.
其中命题正确的是(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学在五次考试中数学成绩统计用茎叶图如表示如图2所示,则甲的平均成绩比乙的平均成绩(填高、低、相等);甲成绩的方差比乙成绩的方差(填大、小) 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=2sin( ![]() ),x∈R的图象只需把函数y=2sinx,x∈R的图象上所有的点( )
),x∈R的图象只需把函数y=2sinx,x∈R的图象上所有的点( )
A.向右平移 ![]() 个单位长度,再把所有各点的横坐标缩短到原来的
个单位长度,再把所有各点的横坐标缩短到原来的 ![]() 倍
倍
B.向左平移 ![]() 个单位长度,再把所有各点的横坐标伸长到原来的3倍
个单位长度,再把所有各点的横坐标伸长到原来的3倍
C.向左平移 ![]() 个单位长度,再把所有各点的横坐标缩短到原来的
个单位长度,再把所有各点的横坐标缩短到原来的 ![]() 倍
倍
D.向右平移 ![]() 个单位长度,再把所有各点的横坐标伸长到原来的3倍
个单位长度,再把所有各点的横坐标伸长到原来的3倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,Sn是其前n项和,
(1)a2=﹣1,S15=75,求an与Sn;
(2)a1+a2+a3+a4=124,an+an﹣1+an﹣2+an﹣3=156,Sn=210,求项数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ< ![]() )的部分图象如图.
)的部分图象如图. 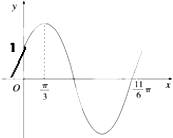
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的 ![]() 倍,再将所得函数图象向右平移
倍,再将所得函数图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间.
个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com