
【题目】△ABC的内角A,B,C的对边分别为a,b,c.已知asin(A+B)=csin![]() .
.
(1)求A;
(2)求sinBsinC的取值范围;
(3)若△ABC的面积为![]() ,周长为8,求a.
,周长为8,求a.
【答案】(1)A![]() (2)(0,
(2)(0,![]() )(3)a
)(3)a![]()
【解析】
(1)用诱导公式和正弦定理化边为角,然后再由二倍角公式变形后可求得![]() ;
;
(2)由(1)可得![]() ,
,![]() ,把
,把![]() 化为
化为![]() 的函数,由三角函数恒等变换化为一个三角函数形式,结合正弦函数性质可得取值范围;
的函数,由三角函数恒等变换化为一个三角函数形式,结合正弦函数性质可得取值范围;
(3)由三角形面积可求得![]() ,由周长及余弦定理得
,由周长及余弦定理得![]() 的三个等式,消去
的三个等式,消去![]() 可解得
可解得![]() .
.
(1)△ABC中,asin(A+B)=csin![]() ,
,
∴asin(π﹣C)=csin(![]() ),
),
∴asinC=ccos![]() ,由正弦定理得sinAsinC=sinCcos
,由正弦定理得sinAsinC=sinCcos![]() ,
,
∴sinA=cos![]() ,即2sin
,即2sin![]() cos
cos![]() cos
cos![]() ;
;
又A∈(0,π),
∴cos![]() 0,
0,
∴2sin![]() 1,即sin
1,即sin![]() ,
,
∴![]() ,
,
解得A![]() ;
;
(2)∵sinBsinC=sinBsin(![]() B)
B)![]() sinBcosB
sinBcosB![]() sin2B
sin2B![]() sin2B
sin2B![]() cos2B
cos2B![]() sin(2B
sin(2B![]() )
)![]() ,
,
又∵B∈(0,![]() ),
),
∴2B![]() ∈(
∈(![]() ,
,![]() ),sin(2B
),sin(2B![]() )∈(
)∈(![]() ,1],
,1],
∴sinBsinC∈(0,![]() ).
).
(3)△ABC的面积为![]() ,周长为8,
,周长为8,
∴![]() bcsinA
bcsinA![]() bc
bc![]() ,
,
∴bc=4,…①
a+b+c=8,…②
由余弦定理得:a2=b2+c2﹣bc,…③
由①②③组成方程组,可得: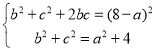 ,
,
可得:(8﹣a)2=a2+12,
解得:a![]() .
.


科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为![]() ,
,![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 与直线
与直线![]() 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若![]() 的面积是
的面积是![]() 面积的2倍,求
面积的2倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为n的样本,得到一周参加社区服务时间的统计数据如下:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(1)求m,n;
(2)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(3)从该校学生中随机调查60名学生,一周参加社区服务时间超过1小时的人数记为X,以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,求X的分布列和数学期望.
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
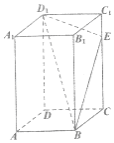
【题目】如图,已知在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 上的一个动点,平面
上的一个动点,平面![]() 与棱
与棱![]() 交于点
交于点![]() ,给出下列命题:
,给出下列命题:
①四棱锥![]() 的体积为20;
的体积为20;
②存在唯一的点![]() ,使截面四边形
,使截面四边形![]() 的周长取得最小值
的周长取得最小值![]() ;
;
③当![]() 点不与
点不与![]() ,
,![]() 重合时,在棱
重合时,在棱![]() 上均存在点
上均存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④存在唯一的点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.
其中正确的命题是_____(填写所有正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过曲线C1:![]() (a>0,b>0)的左焦点F1作曲线C2:x2+y2=a2的切线,设切点为M,直线F1M交曲线C3:y2=2px(p>0)于点N,其中曲线C1与C3有一个共同的焦点,若|MF1|=|MN|,则曲线C1的离心率为( )
(a>0,b>0)的左焦点F1作曲线C2:x2+y2=a2的切线,设切点为M,直线F1M交曲线C3:y2=2px(p>0)于点N,其中曲线C1与C3有一个共同的焦点,若|MF1|=|MN|,则曲线C1的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com