
【题目】已知函数![]() 在
在![]() 与
与![]() 处都取得极值.
处都取得极值.
(1)求![]() 、
、![]() 的值;(2)若对
的值;(2)若对![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用导函数求极值的方法可知![]() ,即可求出
,即可求出![]() ,则不难得到关于
,则不难得到关于![]() 的方程组,解方程组即可求出
的方程组,解方程组即可求出![]() 的值;(2)要使对
的值;(2)要使对![]() 时,
时, ![]() 恒成立,则
恒成立,则![]() 要小于等于
要小于等于![]() 在
在![]() 上的最小值,根据(1)中
上的最小值,根据(1)中![]() 的值,可得到函数
的值,可得到函数![]() ,根据导函数求出函数的单调性,再根据函数
,根据导函数求出函数的单调性,再根据函数![]() 在区间
在区间![]() 两端点的函数值,即可得到最小值,进而可得结果.
两端点的函数值,即可得到最小值,进而可得结果.
试题解析:(1)![]()
![]() 在
在![]() 处都取得极值
处都取得极值
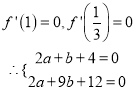 即
即 ![]()
经检验符合
(2)由(1)可知, ![]()
![]()
由![]()
![]() 0,得
0,得![]() 的单调增区间为
的单调增区间为![]() ,由
,由![]()
![]() 0,得
0,得![]() 的单调减区间为
的单调减区间为![]() ∴
∴![]() =1是
=1是![]() 的极大值点 当
的极大值点 当![]() 时,
时, ![]() =
= ![]()
![]() 4,
4, ![]() =3
=3![]() +
+![]() +4
+4
而![]() -
- ![]() =4e-9-
=4e-9-![]() 所以
所以![]() >
> ![]() ,即
,即![]() 在
在![]() 上的最小值为
上的最小值为![]() +4-3e,
+4-3e,
要使对![]() 时,
时, ![]() 恒成立,必须
恒成立,必须![]()
【方法点晴】本题主要考查利用导数求函数的最值以及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.本题是利用方法 ① 求得
恒成立;④ 讨论参数.本题是利用方法 ① 求得![]() 的范围.
的范围.


科目:高中数学 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按![]() 元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第 | 第 | 第 | 第 |
|
收费比例 |
|
|
|
|
|
该公司从注册的会员中, 随机抽取了![]() 位进行统计, 得到统计数据如下:
位进行统计, 得到统计数据如下:
消费次第 | 第 | 第 | 第 | 第 | 第 |
频数 |
|
|
|
|
|
假设汽车美容一次, 公司成本为![]() 元, 根据所给数据, 解答下列问题:
元, 根据所给数据, 解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次, 求这两次消费中, 公司获得的平均利润;
(3)设该公司从至少消费两次, 求这的顾客消费次数用分层抽样方法抽出![]() 人, 再从这
人, 再从这![]() 人中抽出
人中抽出![]() 人发放纪念品, 求抽出
人发放纪念品, 求抽出![]() 人中恰有
人中恰有![]() 人消费两次的概率.
人消费两次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
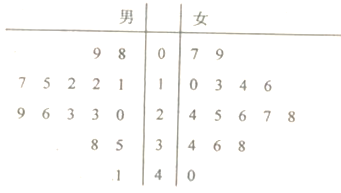
【题目】葫芦岛市某工厂党委为了研究手机对年轻职工工作和生活的影响情况做了一项调查:在厂内用简单随机抽样方法抽取了30名25岁至35岁的职工,对其“每十天累计看手机时间”(单位:小时)进行调查,得到茎叶图如下.所抽取的男职工“每十天累计看手机时间”的平均值和所抽取的女生 “每十天累计看手机时间”的中位数分别是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙、丙、丁、戊、己等6人.(以下问题用数字作答)
(1)邀请这6人去参加一项活动,必须有人去,去几人自行决定,共有多少种不同的情形?
(2)这6人同时加入6项不同的活动,每项活动限1人,其中甲不参加第一项活动,乙不参加第三项活动,共有多少种不同的安排方法?
(3)将这6人作为辅导员安排到3项不同的活动中,每项活动至少安排1名辅导员;求丁、戊、己恰好被安排在同一项活动中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 是两条不同直线,
是两条不同直线, ![]() 、
、![]() 是两个不同平面,则下列四个命题:
是两个不同平面,则下列四个命题:
① 若![]() ,
, ![]() ,
, ![]() ,则
,则![]() ;
;
② 若![]() ,
, ![]() ,则
,则![]() ;
;
③ 若![]() ,
, ![]() ,则
,则![]() 或
或![]() ;
;
④ 若![]() ,
, ![]() ,
, ![]() ,则
,则![]() .
.
其中正确命题的个数为 ( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位射击运动员,在某天训练中已各射击10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
(Ⅰ)通过计算估计,甲、乙二人的射击成绩谁更稳;
(Ⅱ)若规定命中8环及以上环数为优秀,请依据上述数据估计,在第11次射击时,甲、乙人分别获得优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数y=f(x)-log3|x|的零点个数是( )
A.多于4个 B.4个
C.3个 D.2个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量Q之间的关系为:v=a+blog3![]() (其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.
(其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.
(1)求出a,b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2 m/s,则其耗氧量至少要多少个单位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com