
����Ŀ��Ϊ�˽�ѧ��ϲ��У�ڡ�У�չ��������ij��ѧһ����С����ѧУ��һ�꼶�������ʾ����飬�ʾ���100���⣬ÿ��1�֣��ܷ�100�֣��ÿ���С�������ȡ��200��ѧ�����ʾ��ɼ�����λ���֣�����ͳ�ƣ������ݰ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֳ����飬���Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������������60�ֵij�Ϊ
�ֳ����飬���Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������������60�ֵij�Ϊ![]() ��ѧ��������60�ֵij�Ϊ
��ѧ��������60�ֵij�Ϊ![]() ��ѧ��.
��ѧ��.

��1��������֪�����������![]() ���������ܷ��ڷ�����ĸ��ʲ�����
���������ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ�Ա����Ƿ�Ϊ
��ǰ������Ϊ�Ա����Ƿ�Ϊ![]() ��ѧ���й�ϵ��
��ѧ���й�ϵ��
|
| �ϼ� | |
�� | 110 | ||
Ů | 50 | ||
�ϼ� |
��2����Ƶ����Ϊ���ʣ����ڴӸ�У��һѧ��������������ķ���ÿ�γ�ȡ1�ˣ�����ȡ3�Σ��DZ���ȡ��3����![]() ��ѧ��������Ϊ
��ѧ��������Ϊ![]() ����ÿ�γ�ȡ�Ľ����������ģ���
����ÿ�γ�ȡ�Ľ����������ģ���![]() �ķֲ��С�����
�ķֲ��С�����![]() �ͷ���
�ͷ���![]() .
.
�ο���ʽ��![]() ������
������![]() .
.
�ο��ٽ�ֵ��
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡�(1)������������; �ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ�Ա���![]() ��ѧ���й�.
��ѧ���й�.
(2)�ֲ��м�����;![]() ;
;![]() .
.
����������������1����Ƶ�ʷֲ�ֱ��ͼ�ɵ÷�����![]() ��
��![]() ֮���ѧ���������ó�
֮���ѧ���������ó�![]() �������������ù�ʽ�����
�������������ù�ʽ�����![]() �Ĺ۲�ֵ�����������жϣ�
�Ĺ۲�ֵ�����������жϣ�
��2����֪�Ӹ�У��һѧ���������ȡ1�ˣ����ѧ��Ϊ��![]() �ࡱ�ĸ���Ϊ
�ࡱ�ĸ���Ϊ![]() �������õ�
�������õ�![]() �����ö���ֲ���÷ֲ��У���������ѧ������
�����ö���ֲ���÷ֲ��У���������ѧ������
��⣺��1����Ƶ�ʷֲ�ֱ��ͼ�ɵ÷�����![]() ֮���ѧ������Ϊ
֮���ѧ������Ϊ![]() ����
����![]() ֮���ѧ������Ϊ
֮���ѧ������Ϊ![]() �����Ե���60�ֵ�ѧ������Ϊ120.���������Ϊ��
�����Ե���60�ֵ�ѧ������Ϊ120.���������Ϊ��
|
| �ϼ� | |
�� | 80 | 30 | 110 |
Ů | 40 | 50 | 90 |
�ϼ� | 120 | 80 | 200 |
��![]() �Ĺ۲�ֵΪ
�Ĺ۲�ֵΪ![]()
![]() ��
��
�����ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ�Ա���![]() ��ѧ���й�.
��ѧ���й�.
��2����֪�Ӹ�У��һѧ���������ȡ1�ˣ����ѧ��Ϊ��![]() �ࡱ�ĸ���Ϊ
�ࡱ�ĸ���Ϊ![]() .
.
������֪![]() ��
��
����![]()
![]() ��
��
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
��������![]() ������
������![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼��ij�������һ�������ߵ��������̣�����Աÿ��Ӹ��������������ȡ16���������������ߴ磨��λ��cm�������ݳ����������飬������Ϊ��������������״̬������������ijߴ������̬�ֲ�N���̣���2������12�֣�
��1����������״̬��������X��ʾһ���ڳ�ȡ��16���������ߴ��ڣ��̩�3�ң���+3�ң�֮������������P��X��1����X����ѧ������
��2��һ���ڳ������У���������˳ߴ��ڣ��̩�3�ң���+3�ң�֮������������Ϊ��������������һ����������̿��ܳ������쳣�������Ե�����������̽��м�飮
��������˵����������������̷����ĺ����ԣ�
�����������Ǽ���Ա��һ���ڳ�ȡ��16������ijߴ磺
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
������� ![]() =
= ![]() =9.97��s=
=9.97��s= ![]() =
= ![]() ��0.212������xiΪ��ȡ�ĵ�i������ijߴ磬i=1��2������16��
��0.212������xiΪ��ȡ�ĵ�i������ijߴ磬i=1��2������16��
������ƽ���� ![]() ��Ϊ�̵Ĺ���ֵ
��Ϊ�̵Ĺ���ֵ ![]() ������������s��Ϊ�ҵĹ���ֵ
������������s��Ϊ�ҵĹ���ֵ ![]() �����ù���ֵ�ж��Ƿ���Ե�����������̽��м�飿����
�����ù���ֵ�ж��Ƿ���Ե�����������̽��м�飿���� ![]() ��3
��3 ![]() +3
+3 ![]() ��֮������ݣ���ʣ�µ����ݹ��Ʀ̺ͦң���ȷ��0.01����
��֮������ݣ���ʣ�µ����ݹ��Ʀ̺ͦң���ȷ��0.01����
�������������Z������̬�ֲ�N���̣���2������P���̩�3�ң�Z����+3�ң�=0.9974��0.997416��0.9592�� ![]() ��0.09��
��0.09��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ԲN��x2+��y+ ![]() ��2=36��P��ԲN�ϵĵ㣬��Q���߶�NP�ϣ����е�D��0��
��2=36��P��ԲN�ϵĵ㣬��Q���߶�NP�ϣ����е�D��0�� ![]() ����DP�ϵĵ�M������
����DP�ϵĵ�M������ ![]() =2
=2 ![]() ��
�� ![]()
![]() =0��
=0�� 
��1����P��Բ���˶�ʱ�����Q�Ĺ켣���̣�
��2����б��Ϊ ![]() ��ֱ��l�루1��������Q�Ĺ켣���ڲ�ͬ����A��B���ֵ�C��
��ֱ��l�루1��������Q�Ĺ켣���ڲ�ͬ����A��B���ֵ�C�� ![]() ��2�������ABC������ֵʱ��Ӧ��ֱ��l�ķ��̣�
��2�������ABC������ֵʱ��Ӧ��ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г����飬ij����Ʒ�ڽ��ۻ�����ÿ�Ǽ�1Ԫ�����������ͼ���10������֪������Ʒ����Ϊ40Ԫ/��������50Ԫһ���۳�ʱ������500����
��1����д���ۼ�x��![]() ��Ԫ������yԪ֮��ĺ�����ϵʽ��
��Ԫ������yԪ֮��ĺ�����ϵʽ��
��2���Լ��㵱�ۼ۶�Ϊ����Ԫʱ����õ������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ߵ���ѧ��ʦ��ѧ�ڷֱ���![]() ���ֲ�ͬ�Ľ�ѧ��ʽ����ס���������һ�°ࣨ������Ϊ60�ˣ���ѧ��ѧƽ�������������ʶ���ͬ���ڷ̶ܳȺ��Ծ��Զ�һ�������������ȡ�ס��������20���ĸߵ���ѧ��ĩ���Գɼ����õ���Ҷͼ��
���ֲ�ͬ�Ľ�ѧ��ʽ����ס���������һ�°ࣨ������Ϊ60�ˣ���ѧ��ѧƽ�������������ʶ���ͬ���ڷ̶ܳȺ��Ծ��Զ�һ�������������ȡ�ס��������20���ĸߵ���ѧ��ĩ���Գɼ����õ���Ҷͼ��

����������Ҷͼ�ж��ĸ����ƽ���ָߣ�
��������������ߵ���ѧ�ɼ����õ���80�ֵ�ͬѧ�������ȡ����ͬѧ����ɼ�Ϊ86�ֵ�ͬѧ������һ�������еĸ��ʣ�
������ѧУ�涨���ɼ�������85�ֵ�Ϊ���㣬����д�����![]() �����������ж����ܷ��ڷ�����ĸ��ʲ�����0.025��ǰ������Ϊ�ɼ��������ѧ��ʽ�йأ���
�����������ж����ܷ��ڷ�����ĸ��ʲ�����0.025��ǰ������Ϊ�ɼ��������ѧ��ʽ�йأ���
�װ� | �Ұ� | �ϼ� | |
���� | |||
������ | |||
�ϼ� |
�����ٽ�ֵ�������ο���
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽ��![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ex��1��x��ax2 �� ����a=0ʱ����֤��f��x����0��
����x��0ʱ��������ʽf��x����0���������ʵ��a��ȡֵ��Χ��
������x��0��֤����ex��1��ln��x+1����x2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���f��x��=ax2+bx����a��bΪ��������a��0����������f��2-x��=f��x-1�����ҷ���f��x��=x��������ȵ�ʵ����
��1����f��x���Ľ���ʽ��
��2����g��x��=kx+1����F��x��=g��x��-f��x������F��x����[1��2]�ϵ���Сֵ��
��3���Ƿ����ʵ��m��n��m��n����ʹf��x���Ķ������ֵ��ֱ�Ϊ[m��n]��[2m��2n]�������ڣ����m��n��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪��ԲC1��![]() +
+![]() =1��C2��
=1��C2��![]() +
+![]() =1��a��b��0������ͬ�������ʣ�F����
=1��a��b��0������ͬ�������ʣ�F����![]() �� 0��Ϊ��ԲC2���㣬����F��ֱ��l��C1��C2���ν���A��C��D��B�ĵ㣮
�� 0��Ϊ��ԲC2���㣬����F��ֱ��l��C1��C2���ν���A��C��D��B�ĵ㣮
��1������ԲC2�ķ��̣�
��2����֤������ֱ��l����б����α仯����|AC|=|DB|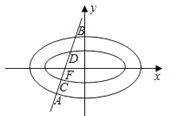
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1����![]() ʱ������
ʱ������![]() �ĵ�������ͼ�ֵ��
�ĵ�������ͼ�ֵ��
��2������������![]() ������
������![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ����
����![]() ��֤����
��֤����![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com