函数y＝x|x|，x∈R，满足( )
A．既是奇函数又是减函数
B．既是偶函数又是增函数
C．既是奇函数又是增函数
D．既是偶函数又是减函数
全能测控一本好卷系列答案
发散思维新课堂系列答案科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：022
函数y＝f(x)是增函数，将y＝f(x)的图象沿x轴方向向右平移2个单位得到图象C，又设
与C关于直线x－y＝0对称，则对应的函数解析式是________．
查看答案和解析>>
科目：高中数学 来源：内蒙古呼伦贝尔市牙克石林业一中2012届高三上学期第二次模拟考试数学文科试题 题型：013
设三次函数f(x)的导函数为
(x)，函数y＝x·(x)的图象的一部分如图所示，则
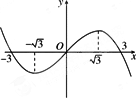
f
(x)的极大值为f(
)，极小值为f(－)
f
(x)的极大值为f(－)，极小值为f()
f
(x)的极大值为f(－3)，极小值为f(3)f
(x)的极大值为f(3)，极小值为f(－3)查看答案和解析>>
科目：高中数学 来源：2013届黑龙江虎林高中高二下学期期中理科数学试卷（解析版） 题型：解答题
已知函数f(x)＝alnx－x2＋1.
(1)若曲线y＝f(x)在x＝1处的切线方程为4x－y＋b＝0，求实数a和b的值；
(2)若a<0，且对任意x1、x2∈(0，＋∞)，都|f(x1)－f(x2)|≥|x1－x2|，求a的取值范围．
【解析】第一问中利用f′(x)＝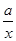
－2x(x>0)，f′(1)＝a－2，又f(1)＝0，所以曲线y＝f(x)在x＝1处的切线方程为y＝(a－2)(x－1)，即(a－2)x－y＋2－a＝0，
由已知得a－2＝4,2－a＝b，所以a＝6，b＝－4.
第二问中，利用当a<0时，f′(x)<0，∴f(x)在(0，＋∞)上是减函数，
不妨设0<x1≤x2，则|f(x1)－f(x2)|＝f(x1)－f(x2)，|x1－x2|＝x2－x1，
∴|f(x1)－f(x2)|≥|x1－x2|等价于f(x1)－f(x2)≥x2－x1，
即f(x1)＋x1≥f(x2)＋x2，结合构造函数和导数的知识来解得。
(1)f′(x)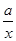＝－2x(x>0)，f′(1)＝a－2，又f(1)＝0，所以曲线y＝f(x)在x＝1处的切线方程为y＝(a－2)(x－1)，即(a－2)x－y＋2－a＝0，
由已知得a－2＝4,2－a＝b，所以a＝6，b＝－4.
(2)当a<0时，f′(x)<0，∴f(x)在(0，＋∞)上是减函数，
不妨设0<x1≤x2，则|f(x1)－f(x2)|＝f(x1)－f(x2)，|x1－x2|＝x2－x1，
∴|f(x1)－f(x2)|≥|x1－x2|等价于f(x1)－f(x2)≥x2－x1，即f(x1)＋x1≥f(x2)＋x2，
令g(x)＝f(x)＋x＝alnx－x2＋x＋1，g(x)在(0，＋∞)上是减函数，
∵g′(x)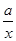＝－2x＋1＝
(x>0)，
∴－2x2＋x＋a≤0在x>0时恒成立，
∴1＋8a≤0，a≤－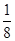
，又a<0，
∴a的取值范围是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
