
(1)当![]() 取最小值时,求
取最小值时,求![]() 的坐标;
的坐标;
(2)当点M满足(1)的条件和结论时,求∠AMB的值.
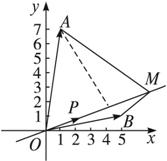
思路分析:因为点M在直线OP上,向量![]() 与
与![]() 共线,可以得到关于OM坐标的一个关系式,再根据
共线,可以得到关于OM坐标的一个关系式,再根据![]() 的最小值,求得
的最小值,求得![]() ,而cos∠AMB是向量
,而cos∠AMB是向量![]() 与
与![]() 夹角的余弦,利用数量积的知识容易解决.
夹角的余弦,利用数量积的知识容易解决.
解:(1)设![]() =(x,y),∵点M在直线OP上,
=(x,y),∵点M在直线OP上,
∴向量![]() 与
与![]() 共线.
共线.
又![]() =(2,1),
=(2,1),
∴x·1-y·2=0,即x=2y.∴![]() =(2y,y).
=(2y,y).
又![]() ,
,![]() =(1,7),
=(1,7),
∴![]() =(1-2y,7-y).
=(1-2y,7-y).
同理![]() =(5-2y,1-y).
=(5-2y,1-y).
于是![]() =(1-2y)(5-2y)+(7-y)(1-y)=4y2-12y+5+y2-8y+7=5y2-20y+12.
=(1-2y)(5-2y)+(7-y)(1-y)=4y2-12y+5+y2-8y+7=5y2-20y+12.
由二次函数的知识,可知当![]() 时,
时,![]() 有最小值-8,此时
有最小值-8,此时![]() =?(4,2).
=?(4,2).
(2)当![]() =(4,2),即y=2时,有
=(4,2),即y=2时,有![]() =(-3,5),
=(-3,5),![]() =(1,-1),|
=(1,-1),|![]() |=34,|
|=34,|![]() |=2,
|=2,
![]() =(-3)×1+5×(-1)=-8,
=(-3)×1+5×(-1)=-8,
∴cos∠AMB= ,
,
即∠AMB=arccos(![]() ).
).
深化升华 对于向量与最值有关的问题,往往是先选取适当的变量,建立关于取定变量的目标关系式(或函数关系式),通过求最值的基本方法求解.如转化成二次函数,或三角函数问题等.也可以利用向量的几何意义求最值.在求向量的夹角时,要注意两个向量的方向性.


科目:高中数学 来源: 题型:

(2)一条直线和一个平面相交,但不______时,这条直线就叫做这个平面的_______,斜线与平面的交点叫做_____.从平面外一点向平面引斜线,这点与________间的线段叫做这点到这个平面的_______.如图所示,直线PR∩α=R,PR不______于α,直线PR是α的一条_____,点R为_______,线段_____是点P到α的______.?
(3)平面外一点到这个平面的垂线段______条,而这点到这个平面的______有无数条.?
(4)从斜线上斜足以外的一点向平面引垂线,过垂足的直线叫做斜线在这个平面内的_______,________与________间的线段叫做这点到平面的斜线段在这个平面内的________.如图所示,直线_____是直线PR在平面α上的______,线段______是点P到平面α的斜线段PR在平面α上的射影.?
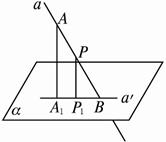
(5)斜线上任意一点在平面上的射影一定在斜线的_____上.事实上,设a是平面α的斜线,B为斜足,在a上任取一点A,作AA1⊥α,A1是垂足,则A1、B确定的直线a′是a在平面α内的______,如图所示,设P是a上任意一点,在a和AA1确定的平面内,作PP1∥AA1,PP1必与a′相交于一点P1.∵AA1α__________ ,PP1______________AA1,∴PP1__________α.P1为P在平面α上的射影,所以点P在平面α上的射影一定在直线a在平面α上的射影a′上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com