
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为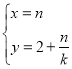 (
(![]() 为参数).设直线
为参数).设直线![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时的点
变化时的点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求出曲线![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设射线
轴正半轴为极轴建立极坐标系,设射线![]() 的极坐标方程为
的极坐标方程为![]() 且
且![]() ,点
,点![]() 是射线
是射线![]() 与曲线
与曲线![]() 的交点,求点
的交点,求点![]() 的极径.
的极径.
科目:高中数学 来源: 题型:
【题目】如图是国家统计局于2020年1月9日发布的2018年12月到2019年12月全国居民消费价格的涨跌幅情况折线图.(注:同比是指本期与同期作对比;环比是指本期与上期作对比.如:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比)根据该折线图,下列结论错误的是( )
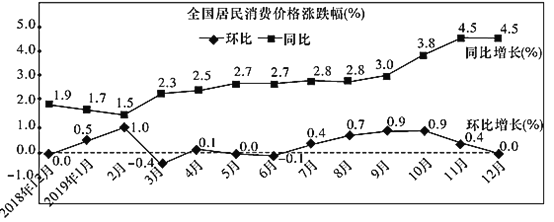
A.2019年12月份,全国居民消费价格环比持平
B.2018年12月至2019年12月全国居民消费价格环比均上涨
C.2018年12月至2019年12月全国居民消费价格同比均上涨
D.2018年11月的全国居民消费价格高于2017年12月的全国居民消费价格
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 中,
中,![]() ,点
,点![]() 在抛物线
在抛物线![]() 上.数列
上.数列![]() 中,点
中,点![]() 在经过点
在经过点![]() ,以
,以![]() 为方向向量的直线
为方向向量的直线![]() 上.
上.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若 ,问是否存在
,问是否存在![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)对任意的正整数![]() ,不等式
,不等式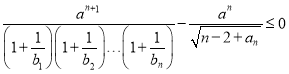 成立,求正数
成立,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为5的菱形ABCD沿对角线AC折起,顶点B移动至![]() 处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
A.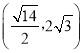 B.
B. C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
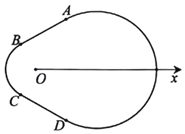
【题目】如图,有一种赛车跑道类似“梨形”曲线,由圆弧![]() 和线段AB,CD四部分组成,在极坐标系Ox中,A(2,
和线段AB,CD四部分组成,在极坐标系Ox中,A(2,![]() ),B(1,
),B(1,![]() ),C(1,
),C(1,![]() ),D(2,
),D(2,![]() ),弧
),弧![]() 所在圆的圆心分别是(0,0),(2,0),曲线M1是弧
所在圆的圆心分别是(0,0),(2,0),曲线M1是弧![]() ,曲线M2是弧
,曲线M2是弧![]() .
.
(1)分别写出M1,M2的极坐标方程:
(2)点E,F位于曲线M2上,且![]() ,求△EOF面积的取值范围.
,求△EOF面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校艺术学院2019级表演专业有27人,播音主持专业9人,影视编导专业18人.某电视台综艺节目招募观众志愿者,现采用分层抽样的方法从上述三个专业的人员中选取6人作为志愿者.
(1)分别写出各专业选出的志愿者人数;
(2)将6名志愿者平均分成三组,且每组的两名同学选自不同的专业,通过适当的方式列出所有可能的结果,并求表演专业的志愿者![]() 与播音主持专业的志愿者分在一组的概率.
与播音主持专业的志愿者分在一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒最近在全国蔓延,具有很强的人与人之间的传染性,该病毒在进入人体后一般有14天的潜伏期,在这14天的潜伏期内患者无任何症状,为病毒传播的最佳时间.假设每位病毒携带者在潜伏期内每天有![]() 位密切接触者,接触病毒携带者后被感染的概率为
位密切接触者,接触病毒携带者后被感染的概率为![]() ,每位密切接触者不用再接触其他病毒携带者.
,每位密切接触者不用再接触其他病毒携带者.
(1)求一位病毒携带者一天内感染的人数![]() 的均值;
的均值;
(2)若![]() ,
,![]() 时,从被感染的第一天算起,试计算某一位病毒携带者在14天潜伏期内,被他平均累计感染的人数(用数字作答);
时,从被感染的第一天算起,试计算某一位病毒携带者在14天潜伏期内,被他平均累计感染的人数(用数字作答);
(3)3月16日20时18分,由我国军事科学院军事科学研究院陈薇院士领衔的科学团队,研制重组新型冠状病毒疫苗获批进入临床状态,新疫苗的使用,可以极大减少感染新型冠状病毒的人数,为保证安全性和有效性,某科研团队抽取500支新冠疫苗,观测其中某项质量指标值,得到如下频率分布直方图:
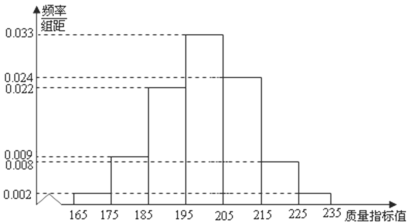
①求这500支该项质量指标值的样本平均值![]() (同一组的数据用该组区代表间的中点值)
(同一组的数据用该组区代表间的中点值)
②由直方图可以认为,新冠疫苗的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算可得这500支新冠疫苗该项指标值的样本方差
,经计算可得这500支新冠疫苗该项指标值的样本方差![]() .现有5名志愿者参与临床试验,观测得出该项指标值分别为:206,178,195,160,229,试问新冠疫苗的该项指标值是否正常,为什么?
.现有5名志愿者参与临床试验,观测得出该项指标值分别为:206,178,195,160,229,试问新冠疫苗的该项指标值是否正常,为什么?
参考数据:![]() ,若
,若![]()
![]() ,则
,则![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆与![]() 轴相切于点
轴相切于点![]() ,过点
,过点![]() ,
,![]() 分别作动圆异于
分别作动圆异于![]() 轴的两切线,设两切线相交于
轴的两切线,设两切线相交于![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)过![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于不同两点
相交于不同两点![]() ,若曲线
,若曲线![]() 上存在点
上存在点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面中,△ABC的两个顶点A、B的坐标分别为A(﹣1,0),B (1,0),平面内两点G、M同时满足下列条件:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ∥
∥![]() ,则△ABC的顶点C的轨迹方程为_____.
,则△ABC的顶点C的轨迹方程为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com