
分析 函数f(x)=sin(ωx+φ)(ω>0,φ∈(0,π))满足$f(\frac{π}{6})=f(\frac{5π}{6})=0$,可得ω($\frac{5π}{6}-\frac{π}{6}$)=nπ,ω=$\frac{3}{2}$n(n∈Z),即可得出结论.
解答 解:函数f(x)=sin(ωx+φ)(ω>0,φ∈(0,π))满足$f(\frac{π}{6})=f(\frac{5π}{6})=0$,
∴ω($\frac{5π}{6}-\frac{π}{6}$)=nπ,∴ω=$\frac{3}{2}$n(n∈Z),
∴①ω=3正确; ②ω≠6k,k∈N*,不正确;③φ可能等于$\frac{3}{4}π$,正确; ④符合条件的ω有无数个,且均为整数,不正确.
故答案为①③.
点评 本题考查三角函数的图象与性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | -8 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
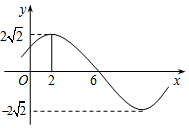
| A. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{3π}{4}$ | B. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{π}{4}$ | C. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{π}{2}$ | D. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 梯形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (1,+∞) | C. | $[\frac{1}{2e-1},+∞)$ | D. | $(\frac{1}{2e-1},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,4-2\sqrt{2}})$ | B. | $({4-2\sqrt{2},2})$ | C. | $({4-2\sqrt{2},\frac{4}{3}}]$ | D. | $({\frac{4}{3},2}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com