
【题目】在直角坐标系中,一个动圆截直线![]() 和
和![]() 所得的弦长分别为8,4.
所得的弦长分别为8,4.
(1)求动圆圆心的轨迹方程![]() ;
;
(2)在轨迹![]() 上是否存在这样的点:它到点
上是否存在这样的点:它到点![]() 的距离等于到点
的距离等于到点![]() 的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】在△ABC中,设边a,b,c所对的角为A,B,C,且A,B,C都不是直角,(bc﹣8)cosA+accosB=a2﹣b2 .
(1)若b+c=5,求b,c的值;
(2)若 ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差为d的等差数列{an}中,已知a1=10,5a1a3=(2a2+2)2 .
(1)求d和an的值;
(2)若d<0,求|a1|+|a2|+|a3|+…+|a2021|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年11月,第十一届中国(珠海)国际航空航天博览会开幕式当天,歼-20的首次亮相给观众留下了极深的印象.某参赛国展示了最新研制的两种型号的无人机,先从参观人员中随机抽取100人对这两种型号的无人机进行评价,评价分为三个等级:优秀、良好、合格.由统计信息可知,甲型号无人机被评为优秀的频率为![]() 、良好的频率为
、良好的频率为![]() ;乙型号无人机被评为优秀的频率为
;乙型号无人机被评为优秀的频率为![]() ,且被评为良好的频率是合格的频率的5倍.
,且被评为良好的频率是合格的频率的5倍.
(1) 求这100人中对乙型号无人机评为优秀和良好的人数;
(2) 如果从这100人中按对甲型号无人机的评价等级用分层抽样的方法抽取5人,然后从其他对乙型号无人机评优秀、良好的人员中各选取1人进行座谈会,会后从这7人中随机抽取2人进行现场操作体验活动,求进行现场操作体验活动的2人都评优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程.
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为了解学生在课外读物方面的支出情况,抽取了n名同学进行调查,结果显示这些同学的支出都在[10,50)(单位:元),其中支出在[30,50)(单位:元)的同学有67人,其频率分布直方图如图所示,则n的值为( )
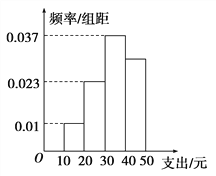
A. 100 B. 120 C. 130 D. 390
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com