
【题目】近年来许多地市空气污染较为严重,现随机抽取某市一年(365天)内100天的![]() 空气质量指数(
空气质量指数(![]() )的监测数据,统计结果如表:
)的监测数据,统计结果如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 4 | 13 | 18 | 30 | 20 | 15 |
记某企业每天由空气污染造成的经济损失为![]() (单位:元),
(单位:元),![]() 指数为
指数为.当
![]() 在区间
在区间![]() 内时,对企业没有造成经济损失;当
内时,对企业没有造成经济损失;当![]() 在区间
在区间![]() 内时,对企业造成的经济损失与
内时,对企业造成的经济损失与![]() 成直线模型(当
成直线模型(当![]() 指数为150时,造成的经济损失为1100元,当
指数为150时,造成的经济损失为1100元,当![]() 指数为200时,造成的经济损失为1400元);当
指数为200时,造成的经济损失为1400元);当![]() 指数大于300时,造成的经济损失为2000元.
指数大于300时,造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取1天,该天经济损失![]() 大于1100且不超过1700元的概率;
大于1100且不超过1700元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,这30天中有8天为严重污染,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该市本年度空气严重污染与供暖有关?
的把握认为该市本年度空气严重污染与供暖有关?
非严重污染 | 严重污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 |
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
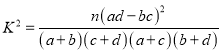 ,其中
,其中![]()
【答案】(1) 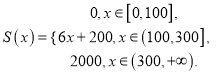 (2)0.4;(3)有
(2)0.4;(3)有![]() 的把握认为该市本年度空气重度污染与供暖有关.
的把握认为该市本年度空气重度污染与供暖有关.
【解析】:
试题分析:(1)根据在区间[0,100]对企业没有造成经济损失;在区间(100,300]对企业造成经济损失成直线模型(当PM2.5指数为150时造成的经济损失为500元,当PM2.5指数为200时,造成的经济损失为700元);当PM2.5指数大于300时造成的经济损失为2000元,可得函数关系式;(2)由500<S≤900,得150<ω≤250,频数为39,即可求出概率;
(3)根据所给的数据,列出列联表,根据所给的观测值的公式,代入数据做出观测值,同临界值进行比较,即可得出结论.
解析:(1)依题意,可得
(2)设“在本年内随机抽取1天,该天经济损失![]() 大于1100元且不超过1700元”为事件
大于1100元且不超过1700元”为事件![]() ,由
,由![]() ,得
,得![]() ,由统计结果,知
,由统计结果,知![]() ,
,
即在本年内随机抽取1天,该天经济损失![]() 大于1100元且不超过1700元的概率为0.4.
大于1100元且不超过1700元的概率为0.4.
(3)根据题中数据可得如下![]() 列联表:
列联表:
非严重污染 | 严重污染 | 合计 | |
供暖季 | 22 | 8 | 30 |
非供暖季 | 63 | 7 | 70 |
合计 | 85 | 15 | 100 |
![]() 的观测值
的观测值![]() ,
,
所以有![]() 的把握认为该市本年度空气重度污染与供暖有关.
的把握认为该市本年度空气重度污染与供暖有关.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中, ![]() ,前
,前![]() 项和
项和![]() 满足
满足![]() (
(![]() ).
).
⑴ 求数列![]() 的通项公式;
的通项公式;
⑵ 记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
⑶ 是否存在整数对![]() (其中
(其中![]() ,
, ![]() )满足
)满足![]() ?若存在,求出所有的满足题意的整数对
?若存在,求出所有的满足题意的整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(I)若![]() ,求函数
,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(II)若函数![]() 在
在![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围;
的取值范围;
(III)令![]() ,
,![]() (
(![]() 是自然对数的底数),求当实数
是自然对数的底数),求当实数![]() 等于多少时,可以使函数
等于多少时,可以使函数![]() 取得最小值为3.
取得最小值为3.
查看答案和解析>>
科目:高中数学 来源: 题型:
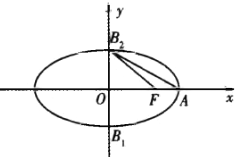
【题目】如图,已知![]() 为椭圆
为椭圆![]() :
: ![]() 的右焦点,
的右焦点, ![]() ,
, ![]() ,
, ![]() 为椭圆的下、上、右三个顶点,
为椭圆的下、上、右三个顶点, ![]() 与
与![]() 的面积之比为
的面积之比为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试探究在椭圆![]() 上是否存在不同于点
上是否存在不同于点![]() ,
, ![]() 的一点
的一点![]() 满足下列条件:点
满足下列条件:点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,
, ![]() 的中点为
的中点为![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,
, ![]() 的中点为
的中点为![]() ,且
,且![]() 的面积为
的面积为![]() .若不存在,请说明理由;若存在,求出点
.若不存在,请说明理由;若存在,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
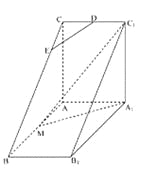
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是由正整数组成的无穷数列,该数列前
是由正整数组成的无穷数列,该数列前![]() 项的最大值记为
项的最大值记为![]() ,第
,第![]() 项之后各项
项之后各项![]() ,
, ![]() ,
, ![]() 的最小值记为
的最小值记为![]() ,
, ![]() .
.
(I)若![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,是一个周期为
,是一个周期为![]() 的数列(即对任意
的数列(即对任意![]() ,
, ![]() ),写出
),写出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(II)设![]() 是正整数,证明:
是正整数,证明: ![]() 的充分必要条件为
的充分必要条件为![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(III)证明:若![]() ,
, ![]() ,则
,则![]() 的项只能是
的项只能是![]() 或者
或者![]() ,且有无穷多项为
,且有无穷多项为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1和BC的中点.
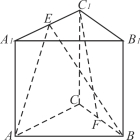
(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F//平面ABE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com