
【题目】随着网上购物的普及,传统的实体店遭受到了强烈的冲击,某商场实体店近九年来的纯利润如下表所示:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
实体店纯利润 | 2 | 2.3 | 2.5 | 2.9 | 3 | 2.5 | 2.1 | 1.7 | 1.2 |
根据这9年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.254;根据后5年的数据,对
作线性相关性检验,求得样本相关系数的绝对值为0.254;根据后5年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.985;
作线性相关性检验,求得样本相关系数的绝对值为0.985;
(1)如果要用线性回归方程预测该商场2019年实体店纯利润,现有两个方案:
方案一:选取这9年的数据,进行预测;
方案二:选取后5年的数据进行预测.
从生活实际背景以及相关性检验的角度分析,你觉得哪个方案更合适.
附:相关性检验的临界值表:
| 小概率 | |
0.05 | 0.01 | |
3 | 0.878 | 0.959 |
7 | 0.666 | 0.798 |
(2)某机构调研了大量已经开店的店主,据统计,只开网店的占调查总人数的![]() ,既开网店又开实体店的占调查总人数的
,既开网店又开实体店的占调查总人数的![]() ,现以此调查统计结果作为概率,若从上述统计的店主中随机抽查了5位,求只开实体店的人数的分布列及期望.
,现以此调查统计结果作为概率,若从上述统计的店主中随机抽查了5位,求只开实体店的人数的分布列及期望.
【答案】(1)选取方案二更合适(2)![]() ,分布列见解析
,分布列见解析
【解析】
(1)根据表中数据的特征及相关系数绝对值的大小可判断方案二更合适.
(2)设只开实体店的店主人数为![]() ,则
,则![]() 服从二项分布,利用公式可得分布列及数学期望.
服从二项分布,利用公式可得分布列及数学期望.
(1)选取方案二更合适,理由如下:
①中介绍了,随着网购的普及,实体店生意受到了强烈的冲击,从表格中的数据可以看出从2014年开始,纯利润呈现逐年下降的趋势,可以预见,2019年的实体店纯利润收入可能会接着下跌,前四年的增长趋势已经不能作为预测后续数据的依据.
②相关系数![]() 越接近1,线性相关性越强,因为根据9年的数据得到的相关系数的绝对值
越接近1,线性相关性越强,因为根据9年的数据得到的相关系数的绝对值![]() ,我们没有理由认为
,我们没有理由认为![]() 与
与![]() 具有线性相关关系;而后5年的数据得到的相关系数的绝对值
具有线性相关关系;而后5年的数据得到的相关系数的绝对值![]() ,所以有
,所以有![]() 的把握认为
的把握认为![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(仅用①解释得3分,仅用②解释或者用①②解释得6分)
(2)此调查统计结果作为概率,从上述统计的店主中随机抽查了1位,开网店的概率为![]() ,只开实体店的概率为
,只开实体店的概率为![]() ,
,
设只开实体店的店主人数为![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以,![]() 的分布列如下:
的分布列如下:
| 0 | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
|
∴![]() ,故
,故![]() .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axlnx﹣x2﹣ax+1(a∈R)在定义域内有两个不同的极值点.
(1)求实数a的取值范围;
(2)设两个极值点分别为x1,x2,x1<x2,证明:f(x1)+f(x2)<2﹣x12+x22.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年新冠肺炎疫情期间,某区政府为了解本区居民对区政府防疫工作的满意度,从本区居民中随机抽取若干居民进行评分(满分
年新冠肺炎疫情期间,某区政府为了解本区居民对区政府防疫工作的满意度,从本区居民中随机抽取若干居民进行评分(满分![]() 分).根据调查数据制成如下表格和频率分布直方图.已知评分在
分).根据调查数据制成如下表格和频率分布直方图.已知评分在![]() 的居民有
的居民有![]() 人.
人.
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
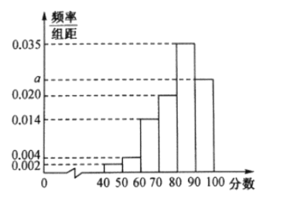
(1)求频率分布直方图中![]() 的值及所调查的总人数;
的值及所调查的总人数;
(2)定义满意度指数![]() (满意程度的平均分)/100,若
(满意程度的平均分)/100,若![]() ,则防疫工作需要进行大的调整,否则不需要大调整.根据所学知识判断该区防疫工作是否需要进行大调整?
,则防疫工作需要进行大的调整,否则不需要大调整.根据所学知识判断该区防疫工作是否需要进行大调整?
(3)为了解部分居民不满意的原因,从不满意的居民(评分在![]() 、
、![]() )中用分层抽样的方法抽取
)中用分层抽样的方法抽取![]() 名居民,倾听他们的意见,并从
名居民,倾听他们的意见,并从![]() 人中抽取
人中抽取![]() 人担任防疫工作的监督员,求这
人担任防疫工作的监督员,求这![]() 人中仅有一人对防疫工作的评分在
人中仅有一人对防疫工作的评分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n为正整数,集合A=![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .对于集合A中的任意元素
.对于集合A中的任意元素![]() 和
和![]() ,记
,记![]() .
.
(Ⅰ)当n=3时,若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值;
的值;
(Ⅱ)当![]() 时,对于
时,对于![]() 中的任意两个不同的元素
中的任意两个不同的元素![]() ,
,![]() ,证明:
,证明:![]() .
.
(Ⅲ)给定不小于2的正整数n,设B是A的子集,且满足:对于B中的任意两个不同元素![]() ,
,![]() ,
,![]() .写出一个集合B,使其元素个数最多,并说明由.
.写出一个集合B,使其元素个数最多,并说明由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二某班共有45人,学号依次为1、2、3、…、45,现按学号用系统抽样的办法抽取一个容量为5的样本,已知学号为6、24、33的同学在样本中,那么样本中还有两个同学的学号应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com