
【题目】已知双曲线![]() :
: ![]() .
.
(1)已知直线![]() 与双曲线
与双曲线![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)过点![]() 作直线
作直线![]() 与双曲线
与双曲线![]() 交于不同的两点
交于不同的两点![]() ,若弦
,若弦![]() 恰被点
恰被点![]() 平分,求直线
平分,求直线![]() 的方程.
的方程.
【答案】(1) m=±2 (2) 4x﹣y﹣2=0
【解析】试题分析:(Ⅰ)分别设A,B的坐标为(x1,y1),(x2,y2),根据弦长公式即可求出,
(Ⅱ)分别设M,N的坐标为(x3,y3),(x4,y4),可得y32﹣![]() x32=1,y42﹣
x32=1,y42﹣![]() x42=1,两式相减,再由中点坐标公式和直线的斜率公式,化简整理可得MN的斜率,再由点斜式方程可得所求直线方程
x42=1,两式相减,再由中点坐标公式和直线的斜率公式,化简整理可得MN的斜率,再由点斜式方程可得所求直线方程
试题解析:
解:(Ⅰ)分别设A,B的坐标为(x1,y1),(x2,y2)
由 ,消y可得,x2﹣4mx+2(m2﹣1)=0,
,消y可得,x2﹣4mx+2(m2﹣1)=0,
∴x1+x2=4m,x1x2=2(m2﹣1),
∴|x1﹣x2|2=(x1+x2)2﹣4x1x2=16m2﹣8(m2﹣1)=8(m2+1),
∴|AB|=![]()
![]() =4
=4![]() ,解得m=±2,
,解得m=±2,
(Ⅱ)分别设M,N的坐标为(x3,y3),(x4,y4),可得y32﹣![]() x32=1,y42﹣
x32=1,y42﹣![]() x42=1,
x42=1,
两式相减,可得(y3﹣y4)(y3+y4)=![]() (x3﹣x4)(x3+x4),
(x3﹣x4)(x3+x4),
由点P(1,2)为MN的中点,
可得x3+x4=2,y3+y4=4,
∴4(y3﹣y4)=![]() ×2(x3﹣x4),∴kMN=
×2(x3﹣x4),∴kMN=![]() =4 经检验
=4 经检验![]()
即直线l的方程为y﹣2=4(x﹣1),即为4x﹣y﹣2=0


科目:高中数学 来源: 题型:
【题目】过双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的右焦点F作渐近线的垂线,设垂足为P(P为第一象限的点),延长FP交抛物线y2=2px(p>0)于点Q,其中该双曲线与抛物线有一个共同的焦点,若
=1(a>0,b>0)的右焦点F作渐近线的垂线,设垂足为P(P为第一象限的点),延长FP交抛物线y2=2px(p>0)于点Q,其中该双曲线与抛物线有一个共同的焦点,若 ![]() =
= ![]() (
( ![]() +
+ ![]() ),则双曲线的离心率的平方为( )
),则双曲线的离心率的平方为( )
A.![]()
B.![]()
C.![]()
+1
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+(a+1)x+a2(a∈R),若f(x)能表示成一个奇函数g(x)和一个偶函数h(x)的和.
(1)求g(x)和h(x)的解析式;
(2)若f(x)和g(x)在区间(-∞,(a+1)2]上都是减函数,求f(1)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别为椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右两个焦点,椭圆上点M(
=1(a>b>0)的左、右两个焦点,椭圆上点M( ![]() ,
, ![]() )到F1、F2两点的距离之和等于4.
)到F1、F2两点的距离之和等于4.
(1)求椭圆C的方程;
(2)已知过右焦点且垂直于x轴的直线与椭圆交于点N(点N在第一象限),E,F是椭圆C上的两个动点,如果kEN+KFN=0,证明直线EF的斜率为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 sin(x+![]() )。
)。
(1)若点P(1,-![]() )在角
)在角![]() 的终边上,求:cos
的终边上,求:cos![]() 和f(
和f(![]() -
-![]() )的值;
)的值;
(2)若x![]() [
[![]() ,
, ![]() ],求f(x)的值域。
],求f(x)的值域。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召![]() 名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成
名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成![]() 组第
组第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示,已知第
,得到的频率分布直方图如图所示,已知第![]() 组有
组有![]() 人.
人.
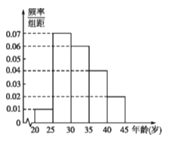
(1)求该组织的人数;
(2)若在第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名志愿者参加某社区的宣传活动,应从第
名志愿者参加某社区的宣传活动,应从第![]() 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(3)在(2)的条件下,该组织决定在这![]() 名志愿者中随机抽取
名志愿者中随机抽取![]() 名志愿者介绍宣传经验,求第
名志愿者介绍宣传经验,求第![]() 组至少有
组至少有![]() 名志愿者被抽中的概率.
名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com