
【题目】在公差为d的等差数列{an}中,已知a1=10,且a1 , 2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
【答案】
(1)解:由题意得 ![]() ,即
,即 ![]() ,整理得d2﹣3d﹣4=0.解得d=﹣1或d=4.
,整理得d2﹣3d﹣4=0.解得d=﹣1或d=4.
当d=﹣1时,an=a1+(n﹣1)d=10﹣(n﹣1)=﹣n+11.
当d=4时,an=a1+(n﹣1)d=10+4(n﹣1)=4n+6.
所以an=﹣n+11或an=4n+6;
(2)解:设数列{an}的前n项和为Sn,因为d<0,由(Ⅰ)得d=﹣1,an=﹣n+11.
则当n≤11时, ![]() .
.
当n≥12时,|a1|+|a2|+|a3|+…+|an|=﹣Sn+2S11= ![]() .
.
综上所述,
|a1|+|a2|+|a3|+…+|an|=  .
.
【解析】(1)直接由已知条件a1=10,且a1 , 2a2+2,5a3成等比数列列式求出公差,则通项公式an可求;(2)利用(1)中的结论,得到等差数列{an}的前11项大于等于0,后面的项小于0,所以分类讨论求d<0时|a1|+|a2|+|a3|+…+|an|的和.
【考点精析】掌握等差数列的通项公式(及其变式)和数列的前n项和是解答本题的根本,需要知道通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系 .
.


科目:高中数学 来源: 题型:
【题目】设F1 , F2分别是椭圆E:x2+ ![]() =1(0<b<1)的左、右焦点,过点F1的直线交椭圆E于A、B两点,若|AF1|=3|F1B|,AF2⊥x轴,则椭圆E的方程为 .
=1(0<b<1)的左、右焦点,过点F1的直线交椭圆E于A、B两点,若|AF1|=3|F1B|,AF2⊥x轴,则椭圆E的方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F为抛物线C:y2=4x的焦点,过点P(﹣1,0)的直线l交抛物线C于两点A,B,点Q为线段AB的中点,若|FQ|=2,则直线l的斜率等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对所有高校学生进行普通话水平测试,发现成绩服从正态分布N(μ,σ2),下表用茎叶图列举出来抽样出的10名学生的成绩.

(1)计算这10名学生的成绩的均值和方差;
(2)给出正态分布的数据:P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544.
由(1)估计从全市随机抽取一名学生的成绩在(76,97)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=x3﹣3x2+3ax﹣3a+3.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当x∈[0,2]时,求|f(x)|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点. 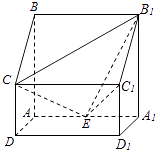
(1)证明B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的正弦值.
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ![]() ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】建设生态文明,是关系人民福祉,关乎民族未来的长远大计.某市通宵营业的大型商场,为响应节能减排的号召,在气温超过![]() 时,才开放中央空调降温,否则关闭中央空调.如图是该市夏季一天的气温(单位:
时,才开放中央空调降温,否则关闭中央空调.如图是该市夏季一天的气温(单位:![]() )随时间(
)随时间(![]() ,单位:小时)的大致变化曲线,若该曲线近似的满足函数
,单位:小时)的大致变化曲线,若该曲线近似的满足函数![]() 关系.
关系.
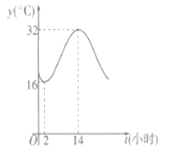
(1)求函数![]() 的表达式;
的表达式;
(2)请根据(1)的结论,判断该商场的中央空调应在本天内何时开启?何时关闭?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com