
分析 (Ⅰ)由条件利用同角三角函数的基本关系、两角和差的三角公式化简所给的式子,求得结果.
(Ⅱ)由条件利用同角三角函数的基本关系、两角和差的三角公式化简所给的式子,求得结果.
解答 解:(Ⅰ)∵$4sinα=-3cosα,且α∈(\frac{π}{2},π)$,∴$tanα=-\frac{3}{4},cosα=-\frac{4}{5},sinα=\frac{3}{5}$,
∴$\frac{{cos(α+\frac{π}{4})}}{sin2α}=\frac{{\frac{{\sqrt{2}}}{2}(cosα-sinα)}}{2sinαcosα}=\frac{{\sqrt{2}}}{4}(\frac{1}{sinα}-\frac{1}{cosα})=\frac{{\sqrt{2}}}{4}(\frac{5}{3}+\frac{5}{4})=\frac{{35\sqrt{2}}}{48}$.
(Ⅱ)已知$\frac{π}{2}$<β<α<$\frac{3π}{4}$,cos(α-β)=$\frac{12}{13}$,sin(α+β)=-$\frac{3}{5}$,∴sin(α-β)=$\frac{5}{13}$,sin(α+β)=-$\frac{4}{5}$,
∴sin2α=sin[(α+β)-(α-β)]=sin(α+β)cos(α-β)+cos(α+β)sin(α-β)=-$\frac{3}{5}$×$\frac{12}{13}$+(-$\frac{4}{5}$)×$\frac{5}{13}$=-$\frac{56}{65}$.
点评 本题主要考查同角三角函数的基本关系、两角和差的三角公式的应用,属于基础题.


科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(理)试卷(解析版) 题型:选择题
若按如图的算法流程图运行后,输出的结果是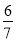 ,则输入的N的值为( )
,则输入的N的值为( )

A.5 B.6 C.7 D.8
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | 4028 | D. | 4030 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com