
���� ��$f��x��=sinx+\sqrt{3}cosx=2��\frac{1}{2}sinx+\frac{{\sqrt{3}}}{2}cosx��=2sin��x+\frac{��}{3}��$���������Һ����ĵ����Կɵú���f��x���������䣬�����жϳ�����
�ڽ�$x=-\frac{��}{6}$����f��x���������жϳ�����
��f��x��=$2sin��x+\frac{��}{3}��$������ƽ�Ƹ�m��m��0����λ���Ⱥ�任Ϊ$y=2sin��x+m+\frac{��}{3}��$���������$m+\frac{��}{3}=\frac{��}{2}+k�У�k��Z��$�������жϳ�����
����ʵ��mʹ�÷���f��x��=m��[0��2��]��ǡ��������ʵ���⣬��Ϻ���$f��x��=2sin��x+\frac{��}{3}��$��y=m��ͼ�ɵó���
���  �⣺��$f��x��=sinx+\sqrt{3}cosx=2��\frac{1}{2}sinx+\frac{{\sqrt{3}}}{2}cosx��=2sin��x+\frac{��}{3}��$���ຯ����������Ϊ$[2k��-\frac{5��}{6}��2k��+\frac{��}{6}]��k��Z��$��
�⣺��$f��x��=sinx+\sqrt{3}cosx=2��\frac{1}{2}sinx+\frac{{\sqrt{3}}}{2}cosx��=2sin��x+\frac{��}{3}��$���ຯ����������Ϊ$[2k��-\frac{5��}{6}��2k��+\frac{��}{6}]��k��Z��$��
�֡�$x��[0��\frac{��}{2}]$����������Ϊ$[0��\frac{��}{6}]$�������ȷ��
�ڽ�$x=-\frac{��}{6}$����f��x����$f��-\frac{��}{6}��=2sin��-\frac{��}{6}+\frac{��}{3}��=1��0$����ڲ���ȷ��
��$f��x��=sinx+\sqrt{3}cosx=2sin��x+\frac{��}{3}��$��������ƽ�Ƹ�m��m��0����λ���Ⱥ�任Ϊ$y=2sin��x+m+\frac{��}{3}��$���������$m+\frac{��}{3}=\frac{��}{2}+k�У�k��Z��$��
��$m��0��m=\frac{��}{6}+k�У�k��N��$�����m����Сֵ��$\frac{��}{6}$�������ȷ��
����ʵ��mʹ�÷���f��x��=m��[0��2��]��ǡ��������ʵ���⣬��Ϻ���$f��x��=2sin��x+\frac{��}{3}��$��y=m��ͼ���֪������x=0��x=2�У���ʱ$f��x��=2sin��x+\frac{��}{3}��=\sqrt{3}$����һ��Ϊ$x=\frac{��}{3}$����x1��x2��x3���� ${x_1}+{x_2}+{x_3}=\frac{7��}{3}$������ȷ��
����֪��ֻ�Т٢ۢ���ȷ��
�ʴ�Ϊ���٢ۢܣ�
���� ���⿼�������Ǻ�����ͼ�������ʡ��Ͳʽ�����������ν�ϵ�˼�뷽����������������������������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
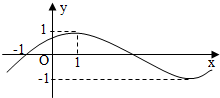 ��֪����f��x��=Asin����x+ϕ����x��R������A��0���أ�0��-$\frac{��}{2}$��ϕ��$\frac{��}{2}$�����䲿��ͼ������ͼ��ʾ����f��x����ͼ�������겻�䣬��������ԭ����$\frac{1}{2}$����������ƽ��1����λ�õ�g��x����ͼ������g��x���Ľ���ʽΪ��������
��֪����f��x��=Asin����x+ϕ����x��R������A��0���أ�0��-$\frac{��}{2}$��ϕ��$\frac{��}{2}$�����䲿��ͼ������ͼ��ʾ����f��x����ͼ�������겻�䣬��������ԭ����$\frac{1}{2}$����������ƽ��1����λ�õ�g��x����ͼ������g��x���Ľ���ʽΪ��������| A�� | g��x��=sin$\frac{��}{8}$��x+1�� | B�� | g��x��=sin��$\frac{��}{2}$x-$\frac{��}{4}$�� | C�� | g��x��=sin��$\frac{��}{8}$x+1�� | D�� | g��x��=sin��$\frac{��}{2}$x+$\frac{��}{4}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Բ | B�� | ������ | C�� | ��Բ | D�� | ˫���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com