[题目]已知定义在R上的函数f(x)=x2+5.记a=f(﹣log25).b=f(log23).c=f(﹣1).则a.b.c的大小关系为( )A.c＜b＜aB.a＜c＜bC.c＜a＜bD.a＜b＜c 题目和参考答案——青夏教育精英家教网—

【题目】已知定义在R上的函数f（x）=x2+5，记a=f（﹣log25），b=f（log23），c=f（﹣1），则a，b，c的大小关系为（）
A.c＜b＜a
B.a＜c＜b
C.c＜a＜b
D.a＜b＜c

【答案】A
【解析】解：∵f（x）是偶函数，∴a=f（﹣log25）=f（log25），c=f（﹣1）=f（1）， ∵log25＞log23＞1，f（x）在（0，+∞）上是增函数，
∴f（log25）＞f（log23）＞f（1），
∴a＞b＞c．
故选：A．
【考点精析】关于本题考查的二次函数的性质和对数值大小的比较，需要了解当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减；几个重要的对数恒等式:，，;常用对数：，即；自然对数：，即（其中…）才能得出正确答案．

练习册系列答案

灵星图书百分百语文阅读组合训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知椭圆C：的右顶点A（2，0），且过点
（1）求椭圆C的方程；
（2）过点B（1，0）且斜率为k1（k1≠0）的直线l于椭圆C相交于E，F两点，直线AE，AF分别交直线x=3于M，N两点，线段MN的中点为P，记直线PB的斜率为k2 ，求证：k1k2为定值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数对任意，都有.

（1）若函数的顶点坐标为且，求的解析式；

（2）函数的最小值记为，求函数在上的值域.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，已知AB⊥平面ACD，DE∥AB，△ACD是等腰三角形，∠CAD=120°，AD=DE=2AB．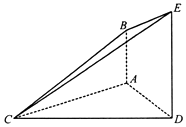
（I）求证：平面BCE⊥平面CDE；
（II）求平面BCE与平面ADEB所成锐二面角的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某乡镇为了提高当地地方经济总量，决定引进资金对原有的两个企业和进行改造，计划每年对两个企业共投资500万元，要求对每个企业至少投资50万元.根据已有经验，改造后企业的年收益（单位：万元）和企业的年收益（单位：万元）与投入资金（单位：万元）分别满足关系式：，.设对企业投资额为（单位：万元），每年两个企业的总收益为（单位：万元）.