
【题目】已知函数f(x)=x2-ax,g(x)=lnx,h(x)=f(x)+g(x).
(1)若函数y=h(x)的单调减区间是![]() ,求实数a的值;
,求实数a的值;
(2)若f(x)≥g(x)对于定义域内的任意x恒成立,求实数a的取值范围.
【答案】(1) a=3.(2) (-∞,1].
【解析】试题分析:(1)对函数求导,已知单调性减区间,故1和![]() 是导函数的两个变号根,h′(1)=h′
是导函数的两个变号根,h′(1)=h′![]() =0,解得a=3,这时只需检验一下在x∈
=0,解得a=3,这时只需检验一下在x∈![]() 时导函数是否小于0即可;(2)原不等式转化为a≤x-
时导函数是否小于0即可;(2)原不等式转化为a≤x-![]() (x>0)恒成立,研究φ(x)=x-
(x>0)恒成立,研究φ(x)=x-![]() 的单调性,求得该函数的最小值即可.
的单调性,求得该函数的最小值即可.
解析:
(1)由题意可知,h(x)=x2-ax+lnx(x>0),
由h′(x)=![]() (x>0),
(x>0),
若h(x)的单调减区间是![]() ,
,
由h′(1)=h′![]() =0,解得a=3,
=0,解得a=3,
而当a=3时,h′(x)=![]() =
=![]() (x>0).
(x>0).
由h′(x)<0,解得x∈![]() ,
,
即h(x)的单调减区间是![]() ,
,
∴a=3.
(2)由题意知x2-ax≥lnx(x>0),
∴a≤x-![]() (x>0).
(x>0).
令φ(x)=x-![]() (x>0),
(x>0),
则φ′(x)=![]() ,
,
∵y=x2+lnx-1在(0,+∞)上是增函数,且x=1时,y=0.
∴当x∈(0,1)时,φ′(x)<0;
当x∈(1,+∞)时,φ′(x)>0,
即φ(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
∴φ(x)min=φ(1)=1,故a≤1.
即实数a的取值范围为(-∞,1].


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 是曲线
是曲线![]() 与直线
与直线![]() :
: ![]() (
(![]() )的交点(异于原点
)的交点(异于原点![]() ).
).
(1)写出![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)求过点![]() 和直线
和直线![]() 垂直的直线
垂直的直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人.
(i)分别求这5人中经常使用、偶尔或不用共享单车的人数;
(ii)从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·南充调研)如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为Li(i=2,3,4),L1=AE,将线段L1,L2,L3,L4竖立放置在同一水平线上,则大致的图形是( )
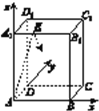
A. 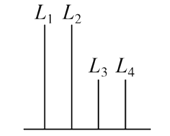 B.
B. 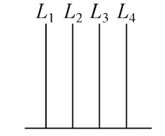
C. 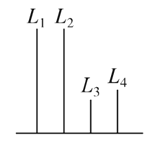 D.
D. 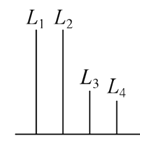
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=-f′(0)ex+2x,点P为曲线y=f(x)在点(0,f(0))处的切线l上的一点,点Q在曲线y=ex上,则|PQ|的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m>0,p:(x+2)(x-6)≤0,q:2-m≤x≤2+m.
(1)若p是q成立的必要不充分条件,求实数m的取值范围;
(2)若![]() 是
是![]() 成立的充分不必要条件,求实数m的取值范围.
成立的充分不必要条件,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com