练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设过原点 O 的直线与圆 C ： 的一个交点为 P ，点 M 为线段 OP 的中点。
    （1）求圆 C 的极坐标方程；
    （2）求点 M 轨迹的极坐标方程，并说明它是什么曲线．

    【答案】
    （1）

    【解答】解：圆 的极坐标方程为


    （2）

    【解答】解：设点 P 的极坐标为 ，点 M 的极坐标为 ，

    ∵点 M 为线段 OP 的中点，∴ ，

    将 ， 代入圆的极坐标方程，得

    ∴点 M 轨迹的极坐标方程为 ，它表示圆心在点 ，半径为 的圆．


    【解析】本题主要考查了圆的极坐标方程，解决问题的关键是(1)根据极坐标和直角坐标的互化公式 可将极坐标方程化为直角坐标方程。(2)因为点 在圆 上则可设 的极坐标为 的极坐标为 ，点 的极坐标为 则 ， 并代入 可得点 的极坐标方程
    【考点精析】本题主要考查了圆的参数方程的相关知识点，需要掌握圆的参数方程可表示为才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知下列三个命题:
    ①若一个球的半径缩小到原来的 ,则其体积缩小到原来的 ;
    ②若两组数据的平均数相等,则它们的标准差也相等;
    ③直线x+y+1=0与圆x2+y2= 相切.
    其中真命题的序号是（ ）
    A.①②③
    B.①②
    C.①③
    D.②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两支球队进行总决赛，比赛采用七场四胜制，即若有一队先胜四场，则此队为总冠军，比赛就此结束.因两队实力相当，每场比赛两队获胜的可能性均为.据以往资料统计，第一场比赛可获得门票收入40万元，以后每场比赛门票收入比上一场增加10万元.

    (I)求总决赛中获得门票总收入恰好为300万元的概率；

    (II)设总决赛中获得门票总收入为X，求X的均值E(X).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知事件在矩ABCD的边CD上随意取一点P，使得△APB的最大边是AB发生的概率为 ，则 = ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

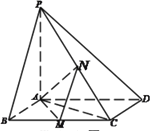
    【题目】如图，已知四棱锥，底面为菱形，，, 平面， 分别是的中点。

    （1）证明： ；

    （2）若为的中点时，与平面所成的角最大，且所成角的正切值为，求点A到平面的距离。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某实验室一天的温度（单位：℃）随时间t（单位：h）的变化近似满足函数关系： f（t）=10﹣ ，t∈[0，24）
    （Ⅰ）求实验室这一天的最大温差；
    （Ⅱ）若要求实验室温度不高于11℃，则在哪段时间实验室需要降温？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=90°．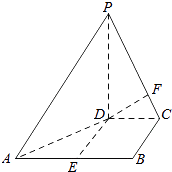
    （1）求证：PC⊥BC；
    （2）求点A到平面PBC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数f（x）是偶函数，且在（﹣∞，0]上是增函数，又f（2）=0，则xf（x）＞0的解集是（ ）
    A.（﹣2，2）
    B.（﹣∞，﹣2）∪（0，2）
    C.（﹣∞，﹣2）∪（2，+∞）
    D.（﹣2，0]∪（2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数f（x），若存在x0∈R，使f（x0）=x0成立，则称x0为函数f（x）的不动点．已知f（x）=x2+bx+c
    （1）若f（x）有两个不动点为﹣3，2，求函数y=f（x）的零点？
    （2）若c= 时，函数f（x）没有不动点，求实数b的取值范围？

    查看答案和解析>>

    同步练习册答案