
分析 (1)先表示出函数的对称轴,求出m的值即可求出函数的解析式,从而求出函数的单调区间;(2)根据函数的单调性求出函数的最值即可.
解答 解:(1)y=-x2+mx-2,x∈[0,5],在x=2处取得最大值.
∴-$\frac{m}{2×(-1)}$=2,解得:m=4,
∴y=-x2+4x-2,
函数在[0,2)递增,在(2,5]递减;
(2)由(1)得:函数在[0,2)递增,在(2,5]递减,
∴x=2时,函数取得最大值:y|x=2=-2×4+8-2=-2,
x=5时,函数取得最小值:y|x=5=-2×25+20-2=-32.
点评 本题考查了二次函数的性质,考查函数的单调性、最值问题,是一道基础题.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:解答题
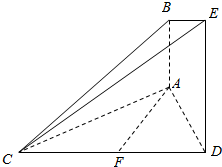 如图所示,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.
如图所示,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(2,+∞) | B. | (1,2) | C. | (1,3) | D. | (-∞,-1)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com