
ЎҫМвДҝЎҝОӘМбёЯіЗКРҫУГсЙъ»оРТёЈёРЈ¬ДііЗКР№«Ҫ»№«ЛҫҙуБҰИ·ұЈ№«Ҫ»іөөДЧјөгВКЈ¬јхЙЩҫУГсіЛіөәтіөКұјдОӘҙЛЈ¬ёГ№«Лҫ¶ФДіХҫМЁіЛҝНөДәтіөКұјдҪшРРНіјЖіЛҝНәтіөКұјдКЬ№«Ҫ»іөЧјөгВКЎўҪ»НЁУө¶ВЗйҝцЎўҪЪјЩИХИЛБчБҝФцҙуөИЗйҝцУ°ПмФЪ№«Ҫ»іөЧјөгВКХэіЈЎўҪ»НЁУө¶ВЗйҝцХэіЈЎў·ЗҪЪјЩИХөДЗйҝцПВЈ¬іЛҝНәтіөКұјдЛж»ъұдБҝ![]() ВъЧгХэМ¬·ЦІј
ВъЧгХэМ¬·ЦІј![]() ФЪ№«Ҫ»іөЧјөгВКХэіЈЎўҪ»НЁУө¶ВЗйҝцХэіЈЎў·ЗҪЪјЩИХөДЗйҝцПВЈ¬өчІйБЛҙуБҝіЛҝНөДәтіөКұјдЈ¬ҫӯ№эНіјЖөГөҪИзНјЖөВК·ЦІјЦұ·ҪНј.
ФЪ№«Ҫ»іөЧјөгВКХэіЈЎўҪ»НЁУө¶ВЗйҝцХэіЈЎў·ЗҪЪјЩИХөДЗйҝцПВЈ¬өчІйБЛҙуБҝіЛҝНөДәтіөКұјдЈ¬ҫӯ№эНіјЖөГөҪИзНјЖөВК·ЦІјЦұ·ҪНј.
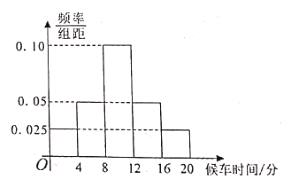
ЈЁ1Ј©ФЪЦұ·ҪНјёчЧйЦРЈ¬ТФёГЧйЗшјдөДЦРөгЦөҙъұнёГЧйЦРөДёчёцЦөЈ¬КФ№АјЖ![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©ФЪНіјЖС§ЦРЈ¬·ўЙъёЕВКөНУЪЗ§·ЦЦ®ИэөДКВјюҪРРЎёЕВККВјюЈ¬Т»°гИПОӘЈ¬ФЪХэіЈЗйҝцПВЈ¬Т»ҙОКФСйЦРЈ¬РЎёЕВККВјюКЗІ»ДЬ·ўЙъөДФЪҪ»НЁУө¶ВЗйҝцХэіЈЎў·ЗҪЪјЩИХөДДіМмЈ¬Лж»ъөчІйБЛёГХҫөД10ГыіЛҝНөДәтіөКұјдЈ¬·ўПЦЖдЦРУР3ГыіЛҝНәтіөКұјді¬№э15·ЦЦУЈ¬КФЕР¶ПёГМ칫Ҫ»іөЧјөгВККЗ·сХэіЈЈ¬ЛөГчАнУЙ.
ЈЁІОҝјКэҫЭЈә![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј©
Ј©
 МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё
МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝMКЗНЦФІTЈә![]() 1ЈЁaЈҫbЈҫ0Ј©ЙПИОТвТ»өгЈ¬FКЗНЦФІTөДУТҪ№өгЈ¬AОӘЧу¶ҘөгЈ¬BОӘЙП¶ҘөгЈ¬OОӘЧшұкФӯөгЈ¬ИзПВНјЛщКҫЈ¬ТСЦӘ|MF|өДЧоҙуЦөОӘ3
1ЈЁaЈҫbЈҫ0Ј©ЙПИОТвТ»өгЈ¬FКЗНЦФІTөДУТҪ№өгЈ¬AОӘЧу¶ҘөгЈ¬BОӘЙП¶ҘөгЈ¬OОӘЧшұкФӯөгЈ¬ИзПВНјЛщКҫЈ¬ТСЦӘ|MF|өДЧоҙуЦөОӘ3![]() Ј¬ЗТЎчMAFГж»эЧоҙуЦөОӘ3
Ј¬ЗТЎчMAFГж»эЧоҙуЦөОӘ3![]() Ј®
Ј®
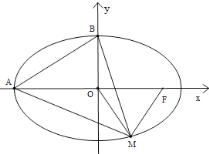
ЈЁ1Ј©ЗуНЦФІTөДұкЧј·ҪіМ
ЈЁ2Ј©ЗуЎчABMөДГж»эөДЧоҙуЦөS0Ј®ИфөгNЈЁxЈ¬yЈ©ВъЧгxЎКZЈ¬yЎКZЈ¬іЖөгNОӘёсөгЈ®ОКНЦФІTДЪІҝКЗ·сҙжФЪёсөгGЈ¬К№өГЎчABGөДГж»эSЎКЈЁ6Ј¬S0Ј©ЈҝИфҙжФЪЈ¬ЗуіцGөДЧшұкЈ¬ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() Ј®
Ј®
ЈЁ1Ј©МЦВЫ![]() өДөҘөчРФІўЦёіцПаУҰөҘөчЗшјдЈ»
өДөҘөчРФІўЦёіцПаУҰөҘөчЗшјдЈ»
ЈЁ2Ј©Иф![]() Ј¬Йи
Ј¬Йи![]() КЗәҜКэ
КЗәҜКэ![]() өДБҪёцј«ЦөөгЈ¬Иф
өДБҪёцј«ЦөөгЈ¬Иф![]() Ј¬ЗТ
Ј¬ЗТ![]() әгіЙБўЈ¬ЗуКөКэkөДИЎЦө·¶О§Ј®
әгіЙБўЈ¬ЗуКөКэkөДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПө![]() ЦРЈ¬ТСЦӘНЦФІC:
ЦРЈ¬ТСЦӘНЦФІC:![]() (
(![]() >
>![]() >0)өДУТҪ№өгОӘF(1Ј¬0)Ј¬ЗТ№эөг(1Ј¬
>0)өДУТҪ№өгОӘF(1Ј¬0)Ј¬ЗТ№эөг(1Ј¬![]() )Ј¬№эөгFЗТІ»Ул
)Ј¬№эөгFЗТІ»Ул![]() ЦбЦШәПөДЦұПЯ
ЦбЦШәПөДЦұПЯ![]() УлНЦФІCҪ»УЪAЈ¬BБҪөгЈ¬өгPФЪНЦФІЙПЈ¬ЗТВъЧг
УлНЦФІCҪ»УЪAЈ¬BБҪөгЈ¬өгPФЪНЦФІЙПЈ¬ЗТВъЧг![]() .
.
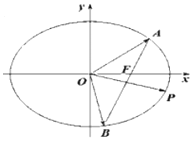
(1)ЗуНЦФІCөДұкЧј·ҪіМЈ»
(2)Иф![]() Ј¬ЗуЦұПЯABөД·ҪіМ.
Ј¬ЗуЦұПЯABөД·ҪіМ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіөШ¶Ф¶¬јҫЦзТ№ОВІоҙуРЎУлДі·ҙјҫҪЪҙу¶№РВЖ·ЦЦ·ўСҝ¶аЙЩЦ®јдөД№ШПөҪшРР·ЦОцСРҫҝЈ¬·ЦұрјЗВјБЛ3ФВ1ИХөҪ3ФВ5ИХөДГҝМмЦзТ№ОВІоУлКөСйКТГҝМмГҝ100ҝЕЦЦЧУЦРөД·ўСҝКэЈ¬өГөҪИзПВЧКБПЈә
ИХЖЪ | 3ФВ1ИХ | 3ФВ2ИХ | 3ФВ3ИХ | 3ФВ4ИХ | 3ФВ5ИХ |
ОВІо | 10 | 11 | 13 | 12 | 8 |
·ўСҝКэyЈЁҝЕЈ© | 23 | 25 | 30 | 26 | 16 |
ЛыГЗЛщИ·¶ЁөДСРҫҝ·Ҫ°ёКЗЈәПИҙУХвОеЧйКэҫЭЦРСЎИЎ2ЧйЈ¬УГКЈПВөД3ЧйКэҫЭЗуПЯРФ»Ш№й·ҪіМЈ¬ФЩ¶ФСЎИЎөД2ЧйКэҫЭҪшРРјмСй.
ЈЁ1Ј©ЗуСЎИЎөД2ЧйКэҫЭЗЎәГКЗПаБЪ2МмКэҫЭөДёЕВКЈ»
ЈЁ2Ј©ИфСЎИЎөДКЗ3ФВ1ИХУл3ФВ5ИХөДБҪЧйКэҫЭЈ¬ЗлёщҫЭ3ФВ2ИХЦБ3ФВ4ИХөДКэҫЭЈ¬Зуіцy№ШУЪxөДПЯРФ»Ш№й·ҪіМЈ»ІўФӨұЁөұОВІоОӘ![]() КұөДЦЦЧУ·ўСҝКэ.
КұөДЦЦЧУ·ўСҝКэ.
ІОҝј№«КҪЈә![]() Ј¬ЖдЦР
Ј¬ЖдЦР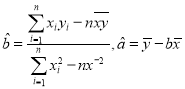
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() Ј¬
Ј¬![]()
ЈЁ1Ј©өұ![]() КұЈ¬Зу
КұЈ¬Зу![]() өДөҘөчЗшјдЈ»
өДөҘөчЗшјдЈ»
ЈЁ2Ј©өұ![]() Ј¬МЦВЫ
Ј¬МЦВЫ![]() өДБгөгёцКэЈ»
өДБгөгёцКэЈ»
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙиәҜКэfЈЁxЈ©ЈҪx©Ғx2+3lnxЈ®
ЈЁўсЈ©ЗуәҜКэfЈЁxЈ©өДј«ЦөЈ»
ЈЁўтЈ©ЦӨГчЈәЗъПЯyЈҪfЈЁxЈ©ФЪЦұПЯyЈҪ2x©Ғ2өДПВ·Ҫ(іэөг![]() Нв)Ј®
Нв)Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() Ј®
Ј®
ЈЁ1Ј©Иф![]() Ј¬ЦӨГчЈәөұ
Ј¬ЦӨГчЈәөұ![]() КұЈ¬
КұЈ¬![]() Ј»өұ
Ј»өұ![]() КұЈ¬
КұЈ¬![]() Ј»
Ј»
ЈЁ2Ј©Иф![]() КЗ
КЗ![]() өДј«ҙуЦөөгЈ¬Зу
өДј«ҙуЦөөгЈ¬Зу![]() Ј®
Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЛДАвЧ¶![]() ЦРЈ¬ЖҪГж
ЦРЈ¬ЖҪГж![]() ЖҪГж
ЖҪГж![]() Ј¬
Ј¬![]() ОӘөИұЯИэҪЗРОЈ¬
ОӘөИұЯИэҪЗРОЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬өг
Ј¬өг![]() КЗ
КЗ![]() өДЦРөгЈ®
өДЦРөгЈ®
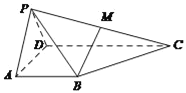
ЈЁ1Ј©ЗуЦӨЈә![]() ЖҪГжPADЈ»
ЖҪГжPADЈ»
ЈЁ2Ј©Зу¶юГжҪЗP©ҒBC©ҒDөДУаПТЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com