练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】(1)求与圆心在直线上，且过点A(2，-3),B(-2，-5)的圆C的方程.

    (2)设是圆C上的点，求的最大值和最小值.

    【答案】(1) 圆C的方程为 （x+1）2+（y+2）2=10,(2) .

    【解析】试题分析：（1）设圆的方程为x2+y2+Dx+Ey+F=0，代入A（2，﹣3），B（﹣2，﹣5），C（0，1），建立方程组，求出D，E，F，即可求出圆的方程；

    （2）利用圆的参数方程求最值；

    试题解析：（1）由于圆心在直线x﹣2y﹣3=0上，故可设圆C的圆心坐标为C（2a+3，a），

    再由圆C经过A（2，﹣3）和B（﹣2，﹣5）两点，

    可得|CA|=|CB|，∴|CA|2=|CB|2，

    ∴（2a+1）2+（a+3）2=（2a+5）2+（a+5）2．

    解得a=﹣2，故圆心C（﹣1，﹣2），半径r=，

    故圆C的方程为 （x+1）2+（y+2）2=10；

    (2)

    , ,

    ,

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆，圆，动圆与圆外切并与圆内切，圆心的轨迹为曲线.

    （1）求的方程；

    （2）是与圆，圆都相切的一条直线，与曲线交于两点，当圆的半径最长时，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

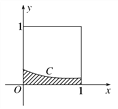
    【题目】在如图所示的正方形中随机投掷10 000个点，则落入阴影部分(曲线C为正态分布

    N(－1,1)的部分密度曲线)的点的个数的估计值为

    附：若X～N(μ，σ2)，则P(μ－σ<X<μ＋σ)＝0.682 6，P(μ－2σ<X<μ＋2σ)＝0.954 4.

    A. 1 193 B. 1 359 C. 2 718 D. 3 413

    查看答案和解析>>

    科目：高中数学 来源： 题型：

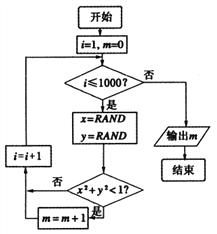
    【题目】我们可以用随机模拟的方法估计的值，如图程序框图表示其基本步骤（函数是产生随机数的函数，它能随机产生内的任何一个实数）．若输出的结果为，则由此可估计的近似值为（ ）

    A. 3.119 B. 3.124 C. 3.132 D. 3.151

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知奇函数在区间上是增函数，且最大值为10，最小值为4，则在区间上的最大值、最小值分别是( )

    A. -4,-10 B. 4,-10

    C. 10,4 D. 不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】袋中有红、白两种颜色的小球共7个，它们除颜色外完全相同，从中任取2个，都是白色小球的概率为，甲、乙两人不放回地从袋中轮流摸取一个小球，甲先取，乙后取，然后再甲取……，直到两人中有一人取到白球时游戏停止，用X表示游戏停止时两人共取小球的个数。

    （1）求；

    （2）求。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示, 四棱锥底面是直角梯形, 底面, 为的中点, .

    (Ⅰ)证明: ;

    (Ⅱ)证明: ;

    (Ⅲ)求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （I）求函数的单调区间；

    （II）若在上恒成立，求实数的取值范围；

    （III）在（II）的条件下，对任意的，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）若对恒成立，求实数的取值范围；

    （2）是否存在整数，使得函数在区间上存在极小值，若存在，求出所有整数的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案