
【题目】已知曲线![]()
(1)若![]() ,过点
,过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若曲线![]() 表示圆时,已知圆
表示圆时,已知圆![]() 与圆
与圆![]() 交于
交于![]() 两点,若弦
两点,若弦![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 为圆
为圆![]() 的直径,且圆
的直径,且圆![]() 过原点,求实数
过原点,求实数![]() 的值.
的值.
【答案】(1)![]() 或
或![]() (即
(即![]() ) ;(2)
) ;(2) ![]() .
.
【解析】试题分析:(1)由已知条件推导出圆心C(1,2),2为半径,由此利用点到直线的距离公式结合已知条件能求出m=1.
(2)求出圆![]() 的方程,两圆相减得公共弦方程
的方程,两圆相减得公共弦方程![]() ,即得m.
,即得m.
试题解析:
(1) 当![]() 时, 曲线C是以
时, 曲线C是以![]() 为圆心,2为半径的圆,
为圆心,2为半径的圆,
若直线![]() 的斜率不存在,显然不符,
的斜率不存在,显然不符,
故可直线![]() 为:
为: ![]() ,即
,即![]() .
.
由题意知,圆心![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,
,
即: ![]()
解得![]() 或
或![]() .故的方程
.故的方程![]() 或
或![]() (即
(即![]() )
)
(2)由曲线C表示圆![]() ,即
,即![]() ,
,
所以圆心C(1,2),半径![]() ,则必有
,则必有![]() .
.
设过圆心![]() 且与
且与![]() 垂直的直线为:
垂直的直线为: ![]() ,解得
,解得![]() ;
;
![]() ,所以,圆心
,所以,圆心![]()
又因为圆![]() 过原点,则
过原点,则![]() ;
;
所以圆![]() 的方程为
的方程为![]() ,整理得:
,整理得: ![]() ;
;
因为![]() 为两圆的公共弦,两圆方程相减得:
为两圆的公共弦,两圆方程相减得: ![]() ;
;
所以![]() 为直线
为直线![]() 的方程;又因为
的方程;又因为![]() ;所以
;所以![]() .
.


科目:高中数学 来源: 题型:
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表和频率分布直方图,回答下面问题:
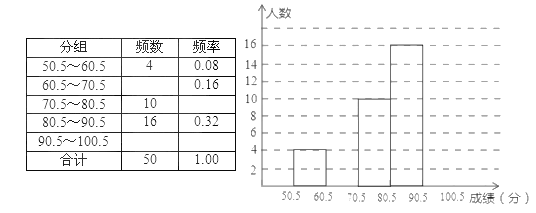
(1)结合图表信息,补全频率分布直方图;
(2)对于参加这次竞赛的900名学生,估计成绩不低于76分的约有多少人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的两个焦点为
)的两个焦点为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() ,
, ![]() 在椭圆上,
在椭圆上, ![]() 在线段
在线段![]() 上,且
上,且![]() 的周长等于
的周长等于![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过圆![]() :
: ![]() 上任意一点
上任意一点![]() 作椭圆
作椭圆![]() 的两条切线
的两条切线![]() 和
和![]() 与圆
与圆![]() 交于点
交于点![]() ,
, ![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,
, ![]() 是焦点,直线
是焦点,直线![]() 是经过点
是经过点![]() 的任意直线.
的任意直线.
(Ⅰ)若直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,且
两点,且![]() (
(![]() 是坐标原点,
是坐标原点, ![]() 是垂足),求动点
是垂足),求动点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)若![]() 、
、![]() 两点在抛物线
两点在抛物线![]() 上,且满足
上,且满足![]() ,求证:直线
,求证:直线![]() 必过定点,并求出定点的坐标.
必过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥中![]() 平面
平面![]() ,且
,且![]() ,
,
![]() .
.
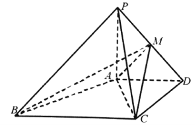
(1)求证:![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为45°,如果存在,求
的大小为45°,如果存在,求![]() 与平面
与平面![]() 所成角的正弦值,如果不存在,请说明理由.
所成角的正弦值,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:设![]() 为每天饮品的销量,
为每天饮品的销量,![]() 为该店每天的利润.
为该店每天的利润.

(1)求![]() 关于
关于![]() 的表达式;
的表达式;
(2)从日利润不少于96元的几天里任选2天,求选出的这2天日利润都是97元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与圆
与圆![]() :
:![]() ,圆
,圆![]()
![]() 都相内切,即圆心
都相内切,即圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ;设
;设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点,![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
,![]() 两个不同的点.
两个不同的点.
(1)求曲线![]() 的方程;
的方程;
(2)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数;若不能,请说明理由.
的比值能否为一个常数?若能,求出这个常数;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com