练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴，建立极坐标系，曲线C1的参数方程为 ，曲线C2的极坐标方程为 ．
    （1）求曲线C1的普通方程和曲线C2的直角坐标方程；
    （2）设P为曲线C1上一点，Q曲线C2上一点，求|PQ|的最小值．

    【答案】
    （1）解：由 消去参数α，得曲线C1的普通方程为 ．

    由 得，曲线C2的直角坐标方程为


    （2）解：设P（2 cosα，2sinα），则

    点P到曲线C2的距离为 ．

    当 时，d有最小值 ，所以|PQ|的最小值为


    【解析】（1）由 消去参数α，得曲线C1的普通方程，利用极坐标与直角坐标的互化方法，得到曲线C2的直角坐标方程；（2）设P（2 cosα，2sinα），利用点到直线的距离公式，即可求|PQ|的最小值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在△ABC中，∠B=45°， ， ，点D是AB的中点，求：
    （1）边AB的长；
    （2）cosA的值和中线CD的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校为了解全校高中学生五一小长假参加实践活动的情况，抽查了100名学生，统计他们假期参加实践活动的时间，绘成的频率分布直方图如图所示．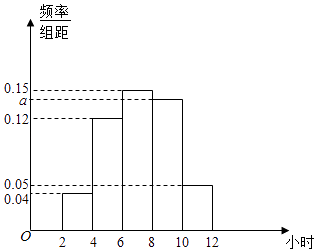

    （1）求这100名学生中参加实践活动时间在6～10小时内的人数；
    （2）估计这100名学生参加实践活动时间的众数、中位数和平均数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司有A、B两个景点，位于一条小路(直道)的同侧，分别距小路 km和2 km，且A、B景点间相距2 km，今欲在该小路上设一观景点，使两景点在同时进入视线时有最佳观赏和拍摄效果，则观景点应设于.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ex（x2+x+a）在（0，f（0））处的切线与直线2x﹣y﹣3=0平行，其中a∈R．
    （1）求a的值；
    （2）求函数f（x）在区间[﹣2，2]上的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC中，A(2，－1)，B(4,3)，C(3，－2)．
    （1）求BC边上的高所在直线的一般式方程；
    （2）求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知矩形ABCD（AB＞AD）的周长为12，若将它关于对角线AC折起后，使边AB与CD交于点P（如图所示），则△ADP面积的最大值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为了对一种新产品进行合理定价，将该产品按亊先拟定的价格进行试销，得到如下数据：

    单价x（元）

    4

    5

    6

    7

    8

    9

    销量V（件）

    90

    84

    83

    80

    75

    68

    由表中数据．求得线性回归方程为 =﹣4x+a．若在这些样本点中任取一点，則它在回归直线右上方的概率为
    （ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】阅读如图程序框图，运行相应的程序，则程序运行后输出的结果为（ ）
    A.7
    B.9
    C.10
    D.11

    查看答案和解析>>

    同步练习册答案