
【题目】设某三棱锥的三视图如图所示,则该三棱锥外接球的表面积为( ) 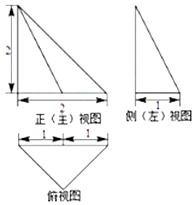
A.4π
B.6π
C.8π
D.10π
【答案】C
【解析】解:根据三视图作出棱锥的直观图如图所示, 由三视图可知底面ABC是等腰直角三角形,AB⊥BC,AC=2,PA⊥平面ABC,PA=2.
∴PC= ![]() =2
=2 ![]() ,
,
取AC的中点D,PC的中点O,连结OD,BD,OB,则OD∥PA,OD= ![]() PA=1,BD=
PA=1,BD= ![]() AC=1,
AC=1,
∴OD⊥平面ABC,∴OA=OC=OP= ![]() PC=
PC= ![]() ,OB=
,OB= ![]() .
.
∴OA=OB=OC=OP= ![]() ,
,
即三棱锥的外接球球心为O,半径为 ![]() .
.
∴外接球的面积S=4π×( ![]() )2=8π.
)2=8π.
故选C.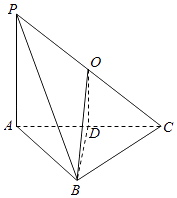
【考点精析】本题主要考查了由三视图求面积、体积的相关知识点,需要掌握求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过8万元时,按销售利润的15%进行奖励;当销售利润超过8万元时,若超出A万元,则超出部分按log5(2A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出奖金y关于销售利润x的关系式;
(2)如果业务员小江获得3.2万元的奖金,那么他的销售利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保局空气质量监控过程中,每隔x天作为一个统计周期.最近x天统计数据如表
空气污染指数 | [0,50] | (50,100] | (100,150] | (150,200] |
天数 | 15 | 40 | 35 | y |
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(Ⅱ)为了创生态城市,该市提出要保证每个统计周期“空气污染指数大于150μg/m3的天数占比不超过15%,平均空气污染指数小于100μg/m3”,请问该统计周期有没有达到预期目标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸A处,发现北偏东45°方向,距A处( ![]() ﹣1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的缉私船奉命以10
﹣1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的缉私船奉命以10 ![]() 海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°的方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间.
海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°的方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. 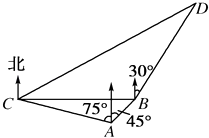
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为![]() .经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
.经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
某厂现有![]() 个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
现有以下四种方案,
方案一:逐个化验;
方案二:平均分成两组化验;
方案三:三个样本混在一起化验,剩下的一个单独化验;
方案四:混在一起化验.
化验次数的期望值越小,则方案的越“优”.
(Ⅰ) 若![]() ,求
,求![]() 个A级水样本混合化验结果不达标的概率;
个A级水样本混合化验结果不达标的概率;
(Ⅱ) 若![]() ,现有
,现有![]() 个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
(Ⅲ) 若“方案三”比“方案四”更“优”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如表所示,求数学成绩在
)之比如表所示,求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC. 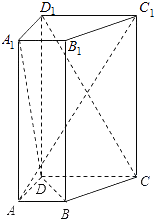
(1)求证:D1C⊥AC1;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中:
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40.
②线性回归直线方程 ![]() 恒过样本中心(
恒过样本中心( ![]() ,
, ![]() ),且至少过一个样本点;
),且至少过一个样本点;
③在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(﹣∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4;
其中真命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com