
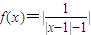 ,且关于x的方程f2(x)+bf(x)+c=0有k(k∈N*)个根,则这k个根的和可能是 .(请写出所有可能值)
,且关于x的方程f2(x)+bf(x)+c=0有k(k∈N*)个根,则这k个根的和可能是 .(请写出所有可能值) 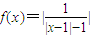 =α,|x-1|=1+
=α,|x-1|=1+ ,此时关于x的方程f2(x)+bf(x)+c=0有2个根,2根之和为2;
,此时关于x的方程f2(x)+bf(x)+c=0有2个根,2根之和为2;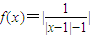 =1,|x-1|=2,或|x-1|=0,此时关于x的方程f2(x)+bf(x)+c=0有3个根,3根之和为3;
=1,|x-1|=2,或|x-1|=0,此时关于x的方程f2(x)+bf(x)+c=0有3个根,3根之和为3;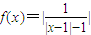 =α,|x-1|=1±
=α,|x-1|=1± ,此时关于x的方程f2(x)+bf(x)+c=0有4个根,4根之和为4;
,此时关于x的方程f2(x)+bf(x)+c=0有4个根,4根之和为4;

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:2011-2012学年山东省潍坊市高二(上)数学寒假作业(3)(解析版) 题型:选择题
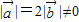 ,且关于x的方程
,且关于x的方程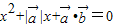 有实根,则
有实根,则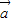 与
与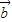 的夹角的取值范围是( )
的夹角的取值范围是( )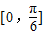
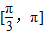
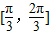
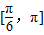
查看答案和解析>>
科目:高中数学 来源:2007-2008学年广东省广州市十校联考高一(下)期中数学试卷(解析版) 题型:选择题
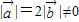 ,且关于x的方程
,且关于x的方程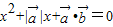 有实根,则
有实根,则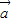 与
与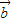 的夹角的取值范围是( )
的夹角的取值范围是( )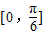
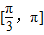
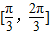
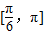
查看答案和解析>>
科目:高中数学 来源:2009-2010学年浙江省金华市永康一中高一(下)期中数学试卷(解析版) 题型:选择题
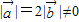 ,且关于x的方程
,且关于x的方程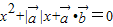 有实根,则
有实根,则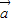 与
与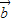 的夹角的取值范围是( )
的夹角的取值范围是( )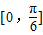
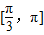
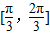
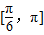
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com