Question

已知直线a与平面α所成的角为15°，点P为空间一定点，过点P作与α成45°、与a成60°的直线l可以作（　　）

A．2条

B．3条

C．4条

D．无数条

Answer 1

分析：设直线a与平面α交于点A，过点A作与α成45°的直线，它在如图的轴截面为等腰直角三角形的圆锥侧面上运动．设a在α内的射影为直线b，a、b确定的平面为β，由直线与平面所成角的性质可得当圆锥的母线在落在平面β内时，它与a所成角为60°或30°．由此将圆锥的母线绕点A旋转并观察母线与直线a所成角的变化，可得圆锥侧面上共有三条母线所在的直线与a所成角为60°，由此结合异面直线所成角的定义可得满足条件的直线l的条数．

解答：解：设直线a与平面α相交于点A，a在α内的射影直线为b，
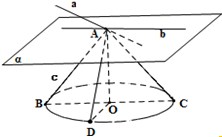
设圆锥的顶点为A点，圆锥的轴AO⊥平面α，圆锥的轴截面为等腰
Rt△ABC，如图所示．
可得图中圆锥的任意一条母线与平面α所成角都等于45°，
设直线c为圆锥的一条母线所在直线，直线a、b确定的平面为β，
由直线与平面所成角的性质，可得当c落在平面β内时，
直线c与直线a所成角等于45°+15°或45°-15°，
当c与AB所在直线重合时，c与a所成角为60°；当c与AC所在直线重合时，c与a所成角为30°．
当直线c从AC的位置按顺时针方向旋转到AB位置时，a、c所成角从30°增大到90°，再减小到60°，
这个过程中必定有一个位置满足c与a所成角为60°；
同理当直线c从AC的位置按逆时针方向旋转到AB位置时，这个过程中也存在一个位置满足c与a所成角为60°．
综上所述，经过点A的直线c共有3条满足c与a所成角为60°．
将满足条件的直线c平移到使它经过空间的点P得到直线l，
根据异面直线所成角的定义，可得直线l与直线a所成角为60°，满足条件的直线l有3条．
∴过点P作与α成45°、与a成60°的直线l可以作3条．
故选：B

点评：本题给出直线a与平面α所成角的大小，求过点P作与α成45°且与a成60°的直线l的条数．着重考查了异面直线所成角的定义及性质直线与平面所成角的性质及其应用等知识，属于中档题．