
【题目】已知a>0且a≠1,函数y=logax,y=ax , y=x+a在同一坐标系中的图象可能是( )
A.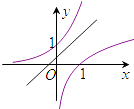
B.
C.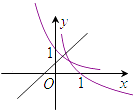
D.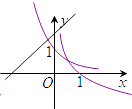
【答案】C
【解析】解:∵函数y=ax与y=logax互为反函数,∴它们的图象关于直线y=x对称.
再由函数y=ax的图象过(0,1),y=logax,的图象过(1,0),
A选项中的y=ax,a>1,y=logax,a>1,但y=x+a中的a<1,不符合题意;
B选项中的y=ax,a>1,y=logax,0<a<1,但y=x+a中的a<1,不符合题意;
C选项中的y=ax,0<a<1,y=logax,0<a<1,但y=x+a中的a<1,符合题意;
D选项中的y=ax,0<a<1,y=logax,0<a<1,但y=x+a中的a>1,不符合题意;
观察图象知,只有C正确.
故答案为:C.
本题考查的是当a>1和0<a<1时指对函数的图像恒过点的问题以及y=x+a一次函数的图像恒过(0,a)和(-a,0)由a的取值范围不同直线的图像不同。


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】已知集合 A={x|﹣1<x<1},B={x|0<x<2},集合 C={x|x>a}.
(1)求集合A UCRB;
(2)若A∩C≠φ,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈R,x﹣2>lgx,命题q:x∈R,x2>0,则( )
A.命题p∨q是假命题
B.命题p∧q是真命题
C.命题p∧(¬q)是真命题
D.命题p∨(¬q)是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,AB⊥AD,CD⊥AD,PA⊥平面ABCD,PA=AD=CD=2AB=2,M为PC的中点. (Ⅰ)求证:BM∥平面PAD;
(Ⅱ)平面PAD内是否存在一点N,使MN⊥平面PBD?若存在,确定点N的位置;若不存在,请说明理由.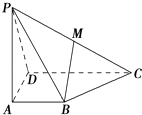
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A城市的出租车计价方式为:若行程不超过3千米,则按“起步价”10元计价;若行程超过3千米,则之后2千米以内的行程按“里程价”计价,单价为1.5元/千米;若行程超过5千米,则之后的行程按“返程价”计价,单价为2.5元/千米.设某人的出行行程为x千米,现有两种乘车方案:①乘坐一辆出租车;②每5千米换乘一辆出租车.
(Ⅰ)分别写出两种乘车方案计价的函数关系式;
(Ⅱ)对不同的出行行程,①②两种方案中哪种方案的价格较低?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线C:y2=4x的焦点,点P是准线l上的动点,直线PF交抛物线C于A,B两点,若点P的纵坐标为m(m≠0),点D为准线l与x轴的交点. (Ⅰ)求直线PF的方程;
(Ⅱ)求△DAB的面积S范围;
(Ⅲ)设 ![]() ,
, ![]() ,求证λ+μ为定值.
,求证λ+μ为定值.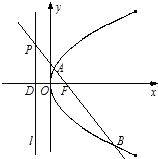
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com