
【题目】已知函数f(x)=|xex|,g(x)=f2(x)+λf(x),若方程g(x)=﹣1有且仅有4个不同的实数解,则实数λ的取值范围是 .
【答案】(﹣∞,﹣e﹣ ![]() )
)
【解析】解:f(x)= ![]() , 当x≥0时,f′(x)=ex+xex=(1+x)ex>0,
, 当x≥0时,f′(x)=ex+xex=(1+x)ex>0,
∴f(x)在[0,+∞)上是增函数,
当x<0时,f′(x)=﹣ex﹣xex=(﹣1﹣x)ex ,
∴当x<﹣1时,f′(x)>0,当﹣1<x<0时,f′(x)<0,
∴f(x)在(﹣∞,﹣1]上是增函数,在(﹣1,0)上是减函数.
当x=﹣1时,f(x)取得极大值f(﹣1)= ![]() .
.
令f(x)=t,
又f(x)≥0,f(0)=0,
则当t<0时,方程f(x)=t无解;
当t=0或t> ![]() 时,方程f(x)=t有一解;
时,方程f(x)=t有一解;
当t= ![]() 时,方程f(x)=t有两解;
时,方程f(x)=t有两解;
当0 ![]() 时,方程f(x)=t有三解.
时,方程f(x)=t有三解.
∵g(x)=f2(x)+λf(x)=﹣1有四个不同的实数解,
∴关于t的方程t2+λt+1=0在(0, ![]() )和(
)和( ![]() ,+∞)上各有一解,
,+∞)上各有一解,
∴ 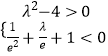 ,解得:λ<﹣e﹣
,解得:λ<﹣e﹣ ![]() .
.
所以答案是(﹣∞,﹣e﹣ ![]() ).
).


科目:高中数学 来源: 题型:
【题目】函数y= ![]() sin(2x+
sin(2x+ ![]() )﹣sinxcosx的单调减区间是( )
)﹣sinxcosx的单调减区间是( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ﹣ ![]() ,kπ﹣
,kπ﹣ ![]() ](k∈Z)
](k∈Z)
C.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
D.[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为提高学生身体素质,决定对毕业班的学生进行身体素质测试,每个同学共有4次测试机会,若某次测试合格就不用进行后面的测试,已知某同学每次参加测试合格的概率组成一个以 ![]() 为公差的等差数列,若他参加第一次测试就通过的概率不足
为公差的等差数列,若他参加第一次测试就通过的概率不足 ![]() ,恰好参加两次测试通过的概率为
,恰好参加两次测试通过的概率为 ![]() .
.
(Ⅰ)求该同学第一次参加测试就能通过的概率;
(Ⅱ)求该同学参加测试的次数的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,由直线x=a,x=a+1(a>0),y=x2及 x 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即 a2< ![]() x2dx<(a+1)2 . 类比之,若对n∈N*,不等式
x2dx<(a+1)2 . 类比之,若对n∈N*,不等式 ![]() <A<
<A< ![]() +
+ ![]() +…+
+…+ ![]() 恒成立,则实数A等于( )
恒成立,则实数A等于( ) 
A.ln ![]()
B.ln 2
C.![]() ln 2
ln 2
D.![]() ln 5
ln 5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}是公差为正数的等差数列,a2和 a5是方程x2﹣12x+27=0 的两实数根,数列{bn}满足3n﹣1bn=nan+1﹣(n﹣1)an .
(Ⅰ)求an与bn;
(Ⅱ)设Tn为数列{bn}的前n项和,求Tn , 并求Tn<7 时n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex﹣1﹣a(x+lnx),a∈R.
(1)若曲线y=f(x)在点(1,f(1))处的切线为x轴,求a的值:
(2)在(1)的条件下,求f(x)的单调区间;
(3)若x>0,f(x)≥f(m)恒成立,且f(m)≥0,求证:f(m)≥2(m2﹣m3).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学校组织的“环保知识”竞赛活动中,甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损,如图:
(Ⅰ)求乙班总分超过甲班的概率;
(Ⅱ)若甲班污损的学生成绩是90分,乙班污损的学生成绩为97分,现从甲乙两班所有选手成绩中各随机抽取2个,记抽取到成绩高于90分的选手的总人数为ξ,求ξ的分布列及数学成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 C1: ![]() =1( a>0,b>0),圆 C2:x2+y2﹣2ax+
=1( a>0,b>0),圆 C2:x2+y2﹣2ax+ ![]() a2=0,若双曲线C1 的一条渐近线与圆 C2 有两个不同的交点,则双曲线 C1 的离心率的范围是( )
a2=0,若双曲线C1 的一条渐近线与圆 C2 有两个不同的交点,则双曲线 C1 的离心率的范围是( )
A.(1, ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.(1,2)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线的中心在坐标原点O,M、N分别为双曲线虚轴的上、下端点,A是双曲线的右顶点,F是双曲线的右焦点,直线AM与FN相交于点P,若∠APF是锐角,则此双曲线的离心率的取值范围是( ) 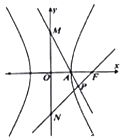
A.( ![]() ,+∞)
,+∞)
B.(1+ ![]() ,+∞)
,+∞)
C.(0, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com