
【题目】(本题![]() 分)
分)
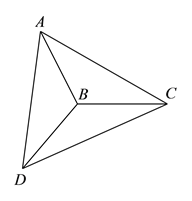
如图, ![]() 和
和![]() 所在的平面互相垂直,且
所在的平面互相垂直,且![]() ,
, ![]() .
.
(Ⅰ)求证: ![]() .
.
(Ⅱ)求直线![]() 与面
与面![]() 所成角的大小的正弦值.
所成角的大小的正弦值.
(Ⅲ)求二面角![]() 的大小的余弦值.
的大小的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】高三理科某班有男同学30名,女同学15名,老师按照分层抽样的方法组建一个6人的课外兴趣小组.
(1)求课外兴趣小组中男、女同学各应抽取的人数;
(2)在一周的技能培训后从这6人中选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选1名同学做实验,求选出的两名同学中恰好仅有一名女同学的概率;
(3)实验结束后,第一次做实验的同学得到的实验数据为1.6、2、1.9、2.5、2,第二次做实验的同学得到的实验数据是2.1、1.8、1.9、2、2.2,请问哪位同学的实验更稳定?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程是
的方程是![]() ,将
,将![]() 向上平移2个单位得到曲线
向上平移2个单位得到曲线![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程为
的参数方程为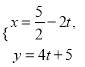 (
(![]() 为参数),判断直线
为参数),判断直线![]() 与曲线
与曲线![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一直角边为股,斜边为弦.若a,b,c为直角三角形的三边,其中c为斜边,则a2+b2=c2,称这个定理为勾股定理.现将这一定理推广到立体几何中:在四面体O-ABC中,∠AOB=∠BOC=∠COA=90°,S为顶点O所对面的面积,S1,S2,S3分别为侧面△OAB,△OAC,△OBC的面积,则下列选项中对于S,S1,S2,S3满足的关系描述正确的为( )
A. S2=S+S+S B. ![]()
C. S=S1+S2+S3 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系内,已知点![]() 及线段
及线段![]() ,在线段
,在线段![]() 上任取一点
上任取一点![]() ,线段
,线段![]() 长度的最小值称为“点
长度的最小值称为“点![]() 到线段
到线段![]() 的距离”,记为
的距离”,记为![]() .
.
(1)设点![]() ,线段
,线段![]()
![]() ,求
,求![]() ;
;
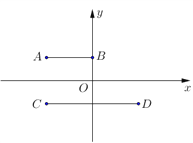
(2)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,线段
,线段![]() ,线段
,线段![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出该函数的值域.
的函数解析式,并写出该函数的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.
组别 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 8 | 0.16 |
第2组 | [60,70) | a | ■ |
第3组 | [70,80) | 20 | 0.40 |
第4组 | [80,90) | ■ | 0.08 |
第5组 | [90,100] | 2 | b |
合计 | ■ | ■ |
(1)求出a,b的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动.
①求所抽取的2名同学中至少有1名同学来自第5组的概率;
②求所抽取的2名同学来自同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设满足以下两个条件的有穷数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 阶“期待数列”:
阶“期待数列”:
①![]() ;
;
②![]() .
.
(![]() )分别写出一个单调递增的
)分别写出一个单调递增的![]() 阶和
阶和![]() 阶“期待数列”.
阶“期待数列”.
(![]() )若某
)若某![]() 阶“期待数列”是等差数列,求该数列的通项公式.
阶“期待数列”是等差数列,求该数列的通项公式.
(![]() )记
)记![]() 阶“期待数列”的前
阶“期待数列”的前![]() 项和为
项和为![]() ,试证:
,试证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com