
【题目】对于定义域为![]() 的函数
的函数![]() ,若同时满足下列三个条件:①
,若同时满足下列三个条件:① ![]() ;② 当
;② 当![]() ,且
,且![]() 时,都有
时,都有 ![]() ;③ 当
;③ 当![]() ,且
,且![]() 时,都有
时,都有![]() , 则称
, 则称![]() 为“偏对称函数”.现给出下列三个函数:
为“偏对称函数”.现给出下列三个函数: ![]() ;
; ![]() ;
; ![]() 则其中是“偏对称函数”的函数个数为
则其中是“偏对称函数”的函数个数为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】(1)经验证可得,函数![]() 都满足条件①;
都满足条件①;
(2)由![]() 可得
可得![]() 或
或![]() ,即条件②等价于函数函数f(x)在区间(∞,0)上单调递减,在区间(0,+∞)上单调递增.
,即条件②等价于函数函数f(x)在区间(∞,0)上单调递减,在区间(0,+∞)上单调递增.
(ⅰ)对于函数![]() ,由于
,由于![]() ,故当
,故当![]() 或
或![]() 时,函数单调递减;当
时,函数单调递减;当![]() 时,函数单调递增.故
时,函数单调递增.故![]() 不满足条件②,从而
不满足条件②,从而![]() 不是“偏对称函数”.
不是“偏对称函数”.
(ⅱ)对于函数![]() ,由于
,由于![]() ,故当
,故当![]() 时,函数
时,函数![]() 单调递减,当
单调递减,当![]() 时,函数
时,函数![]() 单调递增.故
单调递增.故![]() 满足条件②.
满足条件②.
(ⅲ)对于函数![]() ,由复合函数的单调性法则知
,由复合函数的单调性法则知![]() 在区间(∞,0)上单调递减,在(0,+∞)上单调递增,故
在区间(∞,0)上单调递减,在(0,+∞)上单调递增,故![]() 满足条件②.
满足条件②.
(3)由题意可得![]() ,且
,且![]() ,即
,即,且
![]() .
.
(ⅰ)对于函数![]() ,有
,有![]()
![]() .
.
令![]() ,则
,则![]() ,由于
,由于![]() ,故等号不成立,所以
,故等号不成立,所以![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,从而可得
,从而可得![]() .所以
.所以![]() 满足条件③,即
满足条件③,即![]() 是“偏对称函数”.
是“偏对称函数”.
(ⅱ)对于函数![]() ,有
,有![]()
![]() .令
.令![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,从而可得
,从而可得![]() .所以
.所以![]() 满足条件③,即
满足条件③,即![]() 是“偏对称函数”.
是“偏对称函数”.
综上可得函数![]() 和
和![]() 是“偏对称函数”.选C.
是“偏对称函数”.选C.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,AB=BC,D、E分别为
中,AB=BC,D、E分别为![]() 的中点.
的中点.

(1)证明:ED为异面直线BB1与AC1的公垂线段;
(2)设AB=1, ![]() ,求二面角A1—AD—C1的大小.
,求二面角A1—AD—C1的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠BAD=![]() ,AB=BC=
,AB=BC=![]() AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到如图2中△A1BE的位置,得到四棱锥A1-BCDE.
AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到如图2中△A1BE的位置,得到四棱锥A1-BCDE.
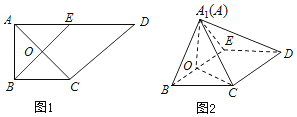
(Ⅰ)证明:CD⊥平面A1OC;
(Ⅱ)当平面A1BE⊥平面BCDE时,四棱锥A1-BCDE的体积为36![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 内一定点,过
内一定点,过![]() 作两条直线交抛物线于
作两条直线交抛物线于![]() ,且
,且![]() 分别是线段
分别是线段![]() 的中点.
的中点.
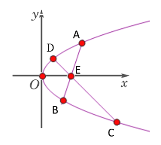
(1)当![]() 时,求△
时,求△![]() 的面积的最小值;
的面积的最小值;
(2)若![]() 且
且![]() ,证明:直线
,证明:直线![]() 过定点,并求定点坐标。
过定点,并求定点坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“既要金山银山,又要绿水青山”。某风景区在一个直径![]() 为
为![]() 米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点
米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点![]() (与
(与![]() 不重合),沿
不重合),沿![]() 修一条直线段小路,在路的两侧(注意是两侧)种植绿化带;再沿弧
修一条直线段小路,在路的两侧(注意是两侧)种植绿化带;再沿弧![]() 修一条弧形小路,在小路的一侧(注意是一侧)种植绿化带,小路与绿化带的宽度忽略不计。
修一条弧形小路,在小路的一侧(注意是一侧)种植绿化带,小路与绿化带的宽度忽略不计。

(1)设![]() (弧度),将绿化带的总长度表示为
(弧度),将绿化带的总长度表示为![]() 的函数
的函数![]() ;
;
(2)求绿化带的总长度![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,且椭圆经过点
,且椭圆经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与圆
与圆![]() 相切:
相切:
(ⅰ)求圆![]() 的标准方程;
的标准方程;
(ⅱ)若直线![]() 过定点
过定点![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() ,与圆
,与圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 (
(![]() ,
, ![]() )展开式的前三项的二项式系数之和为16,所有项的系数之和为1.
)展开式的前三项的二项式系数之和为16,所有项的系数之和为1.
(1)求![]() 和
和![]() 的值;
的值;
(2)展开式中是否存在常数项?若有,求出常数项;若没有,请说明理由;
(3)求展开式中二项式系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在S市的A区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
x(个) | 2 | 3 | 4 | 5 | 6 |
y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间满足的关系式为:![]() ,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店,才能使A区平均每个分店的年利润最大?
,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店,才能使A区平均每个分店的年利润最大?
附:回归方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
![]()
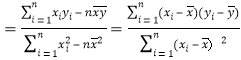 ,
,![]()
![]()
![]()
![]() .
.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com