
【题目】某公司采用招考方式引进人才,规定必须在![]() ,三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点
,三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点![]() 测试合格的概率分别为
测试合格的概率分别为![]() ,小王在上述三个测试点测试合格的概率都是
,小王在上述三个测试点测试合格的概率都是![]() .
.
(1)问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大?请说明理由;
(2)假设小李选择测试点![]() 进行测试,小王选择测试点
进行测试,小王选择测试点![]() 进行测试,记
进行测试,记![]() 为两人在各测试点测试合格的测试点个数之和,求随机变量
为两人在各测试点测试合格的测试点个数之和,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【答案】(1)选择在![]() 测试点(2)
测试点(2)![]()
【解析】
试题分析:(1)问题实质就是求概率最大的两个测试点测试:分三种情况BC,BD,CD;由于各个事件相互独立,所以应用概率乘法公式求概率,因为在![]() 各测试点测试概率为
各测试点测试概率为![]() ,所以选择在
,所以选择在![]() 测试点测试参加面试的可能性最大.(2)先确定随机变量取法:0,1,2,3,4,再分别求对应概率,列表得概率分布,最后根据数学期望公式求数学期望
测试点测试参加面试的可能性最大.(2)先确定随机变量取法:0,1,2,3,4,再分别求对应概率,列表得概率分布,最后根据数学期望公式求数学期望
试题解析:(1)设考生小李在![]() 各测试点测试合格记为事件
各测试点测试合格记为事件![]() ,且各个事件相互独立,由题意
,且各个事件相互独立,由题意![]() .若选择在
.若选择在![]() 测试点测试,则参加面试的概率为:
测试点测试,则参加面试的概率为:![]() ;若选择在
;若选择在![]() 测试点测试,则参加面试的概率为:
测试点测试,则参加面试的概率为:![]() ;若选择在
;若选择在![]() 测试点测试,则参加面试的概率为:
测试点测试,则参加面试的概率为:![]() ;因为
;因为![]() ,所以小李选择在
,所以小李选择在![]() 测试点测试参加面试的可能性最大.
测试点测试参加面试的可能性最大.
(2)记小李在![]() 测试点测试合格记为事件
测试点测试合格记为事件![]() ,记小王在
,记小王在![]() 测试点测试合格记为事件
测试点测试合格记为事件![]() ,
,
则![]() .且
.且![]() 的所有可能取值为0,1,2,3,4
的所有可能取值为0,1,2,3,4
所以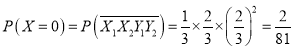 ;
;
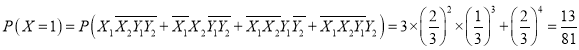 ;
;
![]()
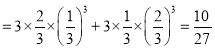 ;
;
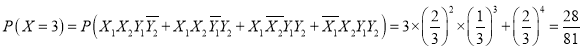 ;
;
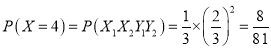 .所以,
.所以,![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() 均为直线,
均为直线,![]() 为平面,下面关于直线与平面关系的命题:
为平面,下面关于直线与平面关系的命题:
①任意给定一条直线与一个平面![]() ,则平面
,则平面![]() 内必存在与
内必存在与![]() 垂直的直线;
垂直的直线;
②![]() 内必存在与
内必存在与![]() 相交的直线;
相交的直线;
③![]() ,必存在与
,必存在与![]() 都垂直的直线;
都垂直的直线;
其中正确命题的个数为( )
A.0个 B.1个
C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级学生身体素质体能测试的成绩(百分制)分布在![]() 内,同时为了了解学生爱好数学的情况,从中随机抽取了
内,同时为了了解学生爱好数学的情况,从中随机抽取了![]() 名学生,这
名学生,这![]() 名学生体能测试成绩的频率分布直方图如图所示,各分数段的“爱好数学”的人数情况如表所示.
名学生体能测试成绩的频率分布直方图如图所示,各分数段的“爱好数学”的人数情况如表所示.

(1)求![]() 的值;
的值;
(2)用分层抽样的方法,从体能成绩在![]() 的“爱好数学”学生中随机抽取6人参加某项活动,现从6人中随机选取2人担任领队,求两名领队中恰有1人体能成绩在
的“爱好数学”学生中随机抽取6人参加某项活动,现从6人中随机选取2人担任领队,求两名领队中恰有1人体能成绩在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若有一个企业,70%的员工年收入1万元,25%的员工年收入3万元,5%的员工年收入11万元,则该企业员工的年收入的平均数是________万元,中位数是________万元,众数是________万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)求![]() 的极值;
的极值;
(2)设![]() ≤
≤![]() ,记
,记![]() 在
在![]() 上的最大值为
上的最大值为![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)设函数![]() (
(![]() 为常数),若使
为常数),若使![]() ≤
≤![]() ≤
≤![]() 在
在![]() 上恒成立的实数
上恒成立的实数![]() 有且只有一个,求实数
有且只有一个,求实数![]() 和
和![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com