
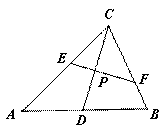
如图,![]() 是
是![]() 的中点,
的中点,![]() ,
,
则![]() .
.
科目:高中数学 来源: 题型:
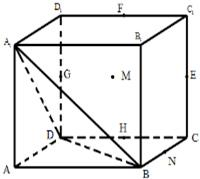 如图,在正方体中,边长为a,EFGH分别是的CC1、C1D1、D1D、DC的中点,N是BC的中点,M在四边形GHEF上及其内部运动,若MH∥平面A1BD,则点M轨迹的长度是( )
如图,在正方体中,边长为a,EFGH分别是的CC1、C1D1、D1D、DC的中点,N是BC的中点,M在四边形GHEF上及其内部运动,若MH∥平面A1BD,则点M轨迹的长度是( )| A、a | ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
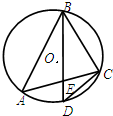 (2011•丹东模拟)选修4-1:几何证明选讲
(2011•丹东模拟)选修4-1:几何证明选讲| 3 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年黑龙江哈师大附中高三上期期中考试文科数学试卷(解析版) 题型:解答题
如图是一个直三棱柱被削去一部分后的几何体的直观图与三视图中的侧视图、俯视图.在直观图中, 是
是 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.

(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求出该几何体的体积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山西忻州一中等四校高三上学期第二次联考文科数学试卷(解析版) 题型:解答题
已知梯形 中
中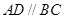 ,
,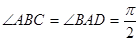 ,
,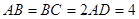 ,
,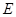 、
、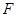 分别是
分别是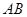 、
、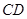 上的点,
上的点,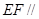
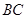 ,
,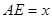 .沿
.沿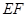 将梯形
将梯形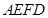 翻折,使平面
翻折,使平面 ⊥平面
⊥平面 (如图).
(如图).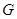 是
是 的中点.
的中点.
(1)当 时,求证:
时,求证: ⊥
⊥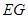 ;
;
(2)当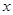 变化时,求三棱锥
变化时,求三棱锥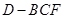 体积的最大值.
体积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com