
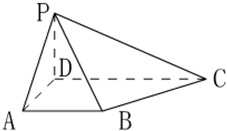
 已知四棱锥P-ABCD的底面为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,PD⊥底面ABCD,平面PBC⊥平面PBD,PA与BC成60°角.
已知四棱锥P-ABCD的底面为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,PD⊥底面ABCD,平面PBC⊥平面PBD,PA与BC成60°角. ,CD=2,
,CD=2,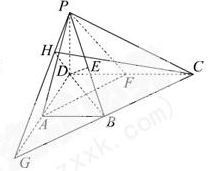
 ,CD=2,
,CD=2,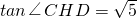 ,
, ;
; ,0),
,0),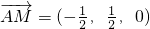 是平面PBD的一个法向量.
是平面PBD的一个法向量. =(-1,a-1,0),
=(-1,a-1,0), =(0,a,-b),
=(0,a,-b),
 ,
, ).
). •n=
•n=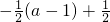 =0,
=0, =(-1,1,0),
=(-1,1,0), =(1,0,-b),
=(1,0,-b),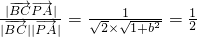 ,
, =(1,0,0)是平面PAD的法向量,
=(1,0,0)是平面PAD的法向量,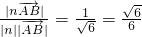 .
. .
. ,CD=2,取CD中点F,连接AF,PF,则∠PAF为PA与BC所成的角,故∠PAF=60°,Rt△ADP≌Rt△FDP,知△PAF为等边三角形,由此能够证明CD=2PD=2.
,CD=2,取CD中点F,连接AF,PF,则∠PAF为PA与BC所成的角,故∠PAF=60°,Rt△ADP≌Rt△FDP,知△PAF为等边三角形,由此能够证明CD=2PD=2. ,0),则AM⊥平面PBD,所以
,0),则AM⊥平面PBD,所以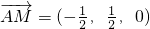 是平面PBD的一个法向量.由
是平面PBD的一个法向量.由 =(-1,a-1,0),
=(-1,a-1,0), =(0,a,-b),得平面PBC的法向量n=(a-1,1,
=(0,a,-b),得平面PBC的法向量n=(a-1,1, ).由此能证明CD=2PD=2.
).由此能证明CD=2PD=2. =(1,0,0)是平面PAD的法向量,能求出侧面PAD与侧面PBC所成锐二面角的大小.
=(1,0,0)是平面PAD的法向量,能求出侧面PAD与侧面PBC所成锐二面角的大小.

科目:高中数学 来源: 题型:
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省济宁一中高三(上)期末数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com