
 如图,在∠AOB的两边上分别为A1、A2、A3、A4和B1、B2、B3、B4、B5共9个点,连接线段AiBi(1≤i≤4,1≤j≤5),如果其中两条线段不相交,则称之为一对“和睦线”,则图中共有( )对“和睦线”
如图,在∠AOB的两边上分别为A1、A2、A3、A4和B1、B2、B3、B4、B5共9个点,连接线段AiBi(1≤i≤4,1≤j≤5),如果其中两条线段不相交,则称之为一对“和睦线”,则图中共有( )对“和睦线” 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
 如图,在∠AOB的两边上分别为A1,A2,A3,A4,B1,B2,B3,B4,B5共9个点,连接线段AiBj(1≤i≤4,1≤j≤5),如果其中两条线段不相交,则称之为一对“和睦线”,则图中共有
如图,在∠AOB的两边上分别为A1,A2,A3,A4,B1,B2,B3,B4,B5共9个点,连接线段AiBj(1≤i≤4,1≤j≤5),如果其中两条线段不相交,则称之为一对“和睦线”,则图中共有查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省连州市高三8月月考理科数学试卷(解析版) 题型:选择题
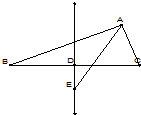
如图,在∠AOB的两边上分别有A1、A2、A3、A4和B1、B2、B3、B4、B5共9个点,连结线段AiBj(1≤i≤4,1≤j≤5),如果其中两条线段不相交,则称之为一对“和睦线”,则图中共有( )对“和睦线”.

A.60 B.62 C.72 D.124
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.60 | B.62 | C.72 | D.124 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com