
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间.
的单调区间.
(2)当![]() 时,讨论函数
时,讨论函数![]() 与
与![]() 图象的交点个数.
图象的交点个数.
【答案】(1)函数![]() 的增区间是
的增区间是![]() ,减区间是
,减区间是![]() ;(2)有一个交点.
;(2)有一个交点.
【解析】分析:(1)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)问题转化为求函数
的减区间;(2)问题转化为求函数![]() 的零点个数问题,通过求导,得到函数
的零点个数问题,通过求导,得到函数![]() 单调区间,求出
单调区间,求出![]() 的极小值,利用数形结合思想、分类讨论思想可求出的函数
的极小值,利用数形结合思想、分类讨论思想可求出的函数![]() 的零点个数即
的零点个数即![]() 和
和![]() 的交点个数.
的交点个数.
详解:(1)函数![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增。
单调递增。
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(2)令![]()
问题等价于求函数![]() 的零点个数,
的零点个数,![]()
当![]() 时,
时,![]() ,有唯一零点.
,有唯一零点.
当![]() ,
,![]()
当![]() 时,
时,![]() ,函数
,函数![]() 为减函数,
为减函数,
注意到![]()
所以![]() 有唯一零点;
有唯一零点;
当![]() 时,
时,![]() 或
或![]() 时
时![]() 时
时![]()
所以函数![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
注意到![]()
所以![]() 有唯一零点;
有唯一零点;
当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
易得![]() ,所以
,所以![]() ,
,
而![]() 所以
所以![]() 有唯一零点;
有唯一零点;
综上,函数![]() 有唯一零点,即两函数图象总有一个交点.
有唯一零点,即两函数图象总有一个交点.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ln(a x)+bx在点(1,f(1))处的切线是y=0;
(I)求函数f(x)的极值;
(II)当![]() 恒成立时,求实数m的取值范围(e为自然对数的底数)
恒成立时,求实数m的取值范围(e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)如图,有一块半椭圆形钢板,其长半轴长为![]() ,短半轴长为
,短半轴长为![]() ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底![]() 是半椭圆的短轴,上底
是半椭圆的短轴,上底![]() 的端点在椭圆上,梯形面积为
的端点在椭圆上,梯形面积为![]() .
.
(1)当![]() ,
,![]() 时,求梯形
时,求梯形![]() 的周长(精确到
的周长(精确到![]() );
);
(2)记![]() ,求面积
,求面积![]() 以
以![]() 为自变量的函数解析式
为自变量的函数解析式![]() ,并写出其定义域.
,并写出其定义域.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.若直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.若直线![]() 的参数方程为
的参数方程为![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,PA⊥平面ABC,则四面体P-ABC的四个面中,直角三角形的个数有( )
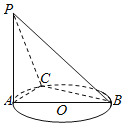
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , Sn=n2+2n,bn=anan+1cos(n+1)π,数列{bn} 的前n项和为Tn , 若Tn≥tn2对n∈N*恒成立,则实数t的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】前不久商丘市因环境污染严重被环保部约谈后,商丘市近期加大环境治理力度,如表提供了商丘某企业节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.

(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=bx+a;
(2)已知该企业技改前100吨甲产品的生产能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低了多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)参考公式:![]() =
= ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F(1,0),点A是直线l1:x=﹣1上的动点,过A作直线l2 , l1⊥l2 , 线段AF的垂直平分线与l2交于点P. (Ⅰ)求点P的轨迹C的方程;
(Ⅱ)若点M,N是直线l1上两个不同的点,且△PMN的内切圆方程为x2+y2=1,直线PF的斜率为k,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com