
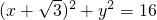 ,点
,点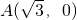 ,Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E.
,Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E.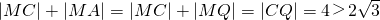
 …(4分)
…(4分)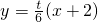 …(6分)
…(6分)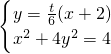 得(9+t2)x2+4t2x+4t2-36=0
得(9+t2)x2+4t2x+4t2-36=0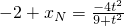 ,∴
,∴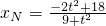
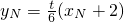 得
得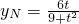 …(8分)
…(8分)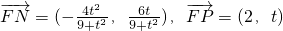
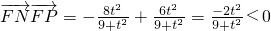 …(10分)
…(10分)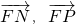 ,利用其数量积小于0,即可得到结论.
,利用其数量积小于0,即可得到结论.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
| 3 |
| OQ |
| OM |
| ON |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:江苏省射阳中学2011-2012学年高一下学期期中考试数学试题 题型:044
在平面直角坐标系xoy中,设直线l的方程为x+my+2m-2=0.
(1)求证:m∈R直线l恒过定点Q,并求出定点Q的坐标;
(2)已知圆C的圆心与定点Q关于直线x-y-2=0对称,过点(1,-1),求圆C的方程;
(3)设M,P是圆C上任意两点,点M关于x轴的对称点为N,若直线MP、NP分别交于x轴于点(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com