
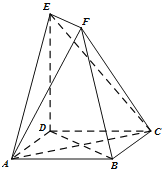
【题目】如图,在多面体ABCDEF中,四边形ABCD为菱形,且![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,且
,且![]() ,
,![]() .
.
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面ACF;
平面ACF;
![]() Ⅱ
Ⅱ![]() 求直线AE与平面ACF所成角的正弦值.
求直线AE与平面ACF所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是24
C. 甲罚球命中率比乙高 D. 乙的众数是21
查看答案和解析>>
科目:高中数学 来源: 题型:
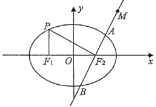
【题目】如图,在平面直角坐标系xOy中,![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左,右焦点,点P是椭圆E上一点,满足
的左,右焦点,点P是椭圆E上一点,满足![]() 轴,
轴,![]() .
.
(1)求椭圆E的离心率;
(2)过点![]() 的直线l与椭圆E交于两点A,B,若在椭圆B上存在点Q,使得四边形OAQB为平行四边形,求直线l的斜率.
的直线l与椭圆E交于两点A,B,若在椭圆B上存在点Q,使得四边形OAQB为平行四边形,求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=![]() .
.
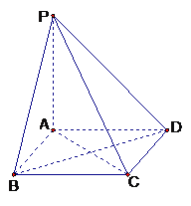
(1)求证:BD⊥平面PAC;
(2)求二面角P—CD—B余弦值的大小;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() 且四个顶点构成面积为
且四个顶点构成面积为![]() 的菱形.
的菱形.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,记
两点,记![]() 中点为
中点为![]() ,坐标原点为
,坐标原点为![]() ,直线
,直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,当四边形
两点,当四边形![]() 的面积为
的面积为![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() 为正实数.
为正实数.
(Ⅰ)若![]() 是函数
是函数![]() 的极值点,讨论函数
的极值点,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若![]() 在
在![]() 上无最小值,且
上无最小值,且![]() 在
在![]() 上是单调增函数,求
上是单调增函数,求![]() 的取值范围,并由此判断曲线
的取值范围,并由此判断曲线![]() 与曲线
与曲线![]() 在
在![]() 交点个数.
交点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】6月12日,上海市发布了《上海市生活垃圾分类投放指南》,将人们生活中产生的大部分垃圾分为七大类.某幢楼前有四个垃圾桶,分别标有“可回收物”、“有害垃圾”、“湿垃圾”、“干垃圾”,小明同学要将鸡骨头(湿垃圾)、贝壳(干垃圾)、指甲油(有害垃圾)、报纸(可回收物)全部投入到这四个桶中,若每种垃圾投放到每个桶中都是等可能的,那么随机事件“4种垃圾中至少有2种投入正确的桶中”的概率是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区选派7名队员代表本区参加全市青少年围棋锦标赛,其中3名来自A学校且1名为女棋手,另外4名来自B学校且2名为女棋手![]() 从这7名队员中随机选派4名队员参加第一阶段的比赛
从这7名队员中随机选派4名队员参加第一阶段的比赛
![]() 求在参加第一阶段比赛的队员中,恰有1名女棋手的概率;
求在参加第一阶段比赛的队员中,恰有1名女棋手的概率;
![]() Ⅱ
Ⅱ![]() 设X为选出的4名队员中A、B两校人数之差的绝对值,求随机变量X的分布列和数学期望
设X为选出的4名队员中A、B两校人数之差的绝对值,求随机变量X的分布列和数学期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com