Question

【题目】已知抛物线的焦点为，直线：交抛物线于两点，．

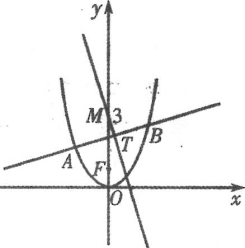
（1）若的中点为，直线的斜率为，证明：为定值；

（2）求面积的最大值．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）设A（x1，y1），B（x2，y2），联立直线与抛物线方程可得：x1＋x2＝4k，即可求得AB的中点坐标为T（2k，1），问题得证。

（2）由弦长公式得：，再求得点M到直线距离为，由（1）可得，即可得，记：，令，则，，利用导数即可求得，问题得解。

（1）证明：联立，消去y得，x2－4kx－4b＝0，

△＝16k2＋16b＞0，即k2＋b＞0，

设A（x1，y1），B（x2，y2），由韦达定理得x1＋x2＝4k，x1x2＝－4b，

因为|AF|＋|BF|＝4，

由抛物线定义得y1＋1＋y2＋1＝4，得y1＋y2＝2，

所以AB的中点坐标为T（2k，1），

所以，

所以．

（2）由（1）得|x1－x2|2＝（x1＋x2）2－4x1x2＝16（k2＋b），

，

设点M到直线距离为d，

则，

而由（1）知，y1＋y2＝kx1＋b＋kx2＋b＝k（x1＋x2）＋2b＝4k2＋2b＝2，

即2k2＋b＝1，即b＝1－2k2，

由△＝16k2＋16b＞0，得0＜k2＜1，

所以

，

记：

令t＝k2，0＜t＜1，则

记

f（t）＝（1＋t）2（1－t）＝1＋t－t2－t3，0＜t＜1，

f'（t）＝1－2t－3t2＝（t＋1）（－3t＋1），

当时，f'（t）＞0，f（t）为增函数；

当时，f'（t）＜0，f（t）为减函数；

当，，

所以，S△ABM的最大值为．