柜子里有4双不同的鞋,随机地取出4只,试求下列事件的概率.
(1)取出的鞋子都不成对;(2)取出的鞋恰好有两只成对;(3)取出的鞋至少有两只成对;(4)取出的鞋全部成对.
解:从4双不同的鞋中随机地取出4只,共有C
84=70个基本事件,且这些基本事件发生的可能性相同.
(1)记“取出的鞋都不成对”为事件A,其包含2×2×2×2=16个基本事件.
所以,由古典概型概率公式得P(A)=
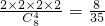
.
(2)记“取出的鞋恰好有两只是成对的”为事件B,其包含 C
41•C
32•2•2=48个基本事件.
所以,由古典概型概率公式得P(B)=

=

.
(3)记“取出的鞋至少有两只成对”为事件C,其对立事件为

:“取出的鞋都不成对”,P(

)=
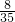
.
所以,P(C)=1-P(

)=1-
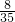
=

.
(4)记“取出的鞋全部成对”为事件D,其包含 C
42=6个基本事件,
故P(D)=

=
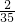
.
分析:(1)由题意知本题是一个古典概型,试验包含的所有事件是从8只鞋里选4只,记“取出的鞋都不成对”为事件A,根据乘法原理得出其包含的基本事件数,根据事件的概率公式得到结果.
(2)本题是一个古典概型,试验包含的所有事件是从8只鞋里选4只,记“取出的鞋恰好有两只是成对的”为事件B,根据乘法原理得出其包含的基本事件数,根据事件的概率公式得到结果.
(3)由题意知本题是一个古典概型,试验包含的所有事件是从8只鞋里选4只,记“取出的鞋至少有两只成对”为事件C,其对立事件为

:“取出的鞋都不成对”,且P(

)=
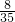
,由P(C)=1-P(

),运算得到结果.
(4)从4双不同的鞋中随机地取出4只,共有C
84 =70个基本事件,记“取出的鞋全部成对”为事件D,其包含 C
42=6个基本事件,由此求得事件D的概率.
点评:本题主要考查古典概型和对立事件,正难则反是解题时要时刻注意的,我们尽量用简单的方法来解题,这样可以避免一些繁琐的运算,使得题目看起来更加清楚,体现了转化的数学思想,属于基础题.

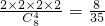 .
. =
= .
. :“取出的鞋都不成对”,P(
:“取出的鞋都不成对”,P( )=
)=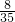 .
. )=1-
)=1-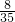 =
= .
.  =
=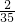 .
. :“取出的鞋都不成对”,且P(
:“取出的鞋都不成对”,且P( )=
)=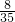 ,由P(C)=1-P(
,由P(C)=1-P( ),运算得到结果.
),运算得到结果.
